
题目列表(包括答案和解析)
20. (本题满分14分)
已知椭圆C的中心在原点,焦点在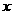 轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形(记为Q).
轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形(记为Q).
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P是椭圆C的左准线与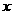 轴的交点,过点P的直线
轴的交点,过点P的直线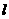 与椭圆C相交于M,N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线
与椭圆C相交于M,N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线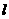 的斜率的取值范围。
的斜率的取值范围。
19. (本题满分14分)
已知二次函数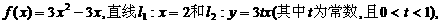
直线l2与函数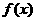 的图象以及直线l1、l2与函数
的图象以及直线l1、l2与函数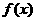 的图象所围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为
的图象所围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为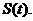
(I)求函数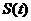 的解析式;
的解析式;
(II)定义函数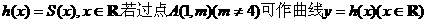 的三条切线,求实数m的取值范围。
的三条切线,求实数m的取值范围。
18. (本题满分14分)
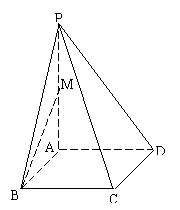 如图,在四棱锥
如图,在四棱锥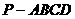 中,底面
中,底面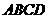 是
是
边长为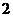 的菱形,
的菱形,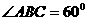 ,
,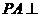 平面
平面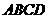 ,
,
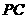 与平面
与平面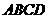 所成角的大小为
所成角的大小为 ,
,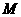 为
为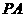 的中点.
的中点.
(1)求四棱锥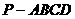 的体积;
的体积;
(2)求异面直线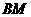 与
与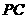 所成角的大小(结果用
所成角的大小(结果用
反三角函数表示)
17. (本题满分12分)
某学校举办一场以“为希望工程献爱心”为主题的图书义卖活动,同学甲随机地从10本书中买两本,假设每本书被甲同学买走的概率相同,已知这10本书中有3本单价定为10元,4本单价定为15元,3本单价定为20元,记甲同学买这两本书所付金额为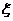 (元)。求:
(元)。求:
(Ⅰ)随机变量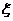 的分布列;
的分布列;
(Ⅱ)随机变量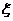 的期望
的期望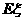 和方差
和方差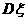 。
。
16. (本题满分12分)
已知函数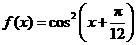 ,
,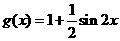 .设
.设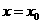 是函数
是函数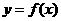 图象的一条对称轴,求
图象的一条对称轴,求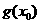 的值.
的值.
(2)已知函数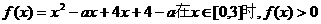 成立,求a的取值范围。
成立,求a的取值范围。
(二)选做题(13 ~ 15题,考生只能从中选做两题)
13. (坐标系与参数方程选做题)在极坐标系中,过圆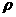 =6cos
=6cos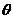 的圆心,且垂直于极轴的直线的极坐标方程为
的圆心,且垂直于极轴的直线的极坐标方程为
14. (不等式选讲选做题)|2x-3|+|3x+2|的最小值是
15. (几何证明选讲选做题) 已知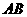 是半圆
是半圆 的直径,点
的直径,点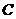 在半圆上,
在半圆上,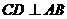 于点
于点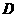 ,且
,且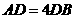 ,设
,设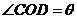 ,则
,则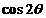 =
.
=
.
(一)必做题(9 ~ 12题)
9. 在(x-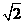 )2006 的二项展开式中,含x的奇次幂的项之和为S,当x=
)2006 的二项展开式中,含x的奇次幂的项之和为S,当x=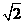 时,S等于
时,S等于
10. 右图中有一个信号源和五个接收器。接收器与信号源在同一个串联线路中时,就能接收到信号,否则就不能接收到信号。若将图中左端的六个接线点随机地平均分成三组,将右端的六个接线点也随机地平均分成三组,再把所有六组中每组的两个接线点用导线连接,则这五个接收器能同时接收到信号的概率是
11. 下列四个条件中,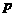 是
是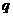 的充要条件条件的是
的充要条件条件的是
①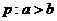 ,
,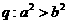
②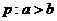 ,
,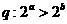
③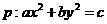 为双曲线,
为双曲线,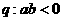
④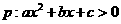 ,
,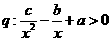
⑤ 或
或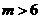 ;
;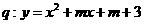 有两个不同的零点。
有两个不同的零点。
12. 在数列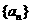 在中,
在中,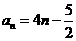 ,
,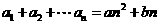 ,
,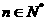 ,其中
,其中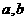 为常数,则
为常数,则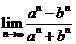 的值是 .
的值是 .
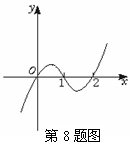
8. 已知函数f(x)=ax3+bx2+cx+d的图象如图2-3,则( )
A.b∈(-∞,0)
B.b∈(0,1)
C.b∈(1,2)
D.b∈(2,+∞)
7. 从2004名学生中选取50名组成参观团,若采用下面的方法选取:先用简单随机抽样从2004人中剔除4人,剩下的2000人再按系统抽样的方法进行,则每人入选的概率
从2004名学生中选取50名组成参观团,若采用下面的方法选取:先用简单随机抽样从2004人中剔除4人,剩下的2000人再按系统抽样的方法进行,则每人入选的概率
A.不全相等 B.均不相等 C.都相等且为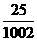 D.都相等且为
D.都相等且为
6. 已知(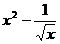 )
)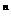 的展开式中第三项与第五项的系数之比为
的展开式中第三项与第五项的系数之比为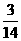 ,则展开式中常数项是
,则展开式中常数项是
(A)-1 (B)1 (C)-45 (D)45
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com