
题目列表(包括答案和解析)
20.(本题满分16分)
若函数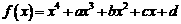 .
.
(1)当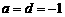 ,
,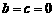 时,若函数
时,若函数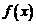 的图象与
的图象与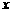 轴所有交点的横坐标的和与积分别为
轴所有交点的横坐标的和与积分别为 ,
,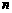 .
.
(i)求证: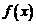 的图象与
的图象与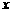 轴恰有两个交点;
轴恰有两个交点;
(ii)求证: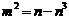 .
.
(2)当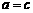 ,
,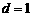 时,设函数
时,设函数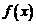 有零点,求
有零点,求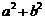 的最小值.
的最小值.
解:(1)(i)因为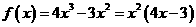 ,
,
所以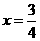 是使
是使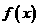 取到最小值的唯一的值,且在区间
取到最小值的唯一的值,且在区间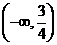 上,函数
上,函数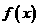 单调递减;在区间
单调递减;在区间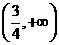 上,函数
上,函数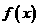 单调递增.因为
单调递增.因为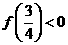 ,
,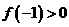 ,
,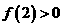 ,所以
,所以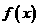 的图象与x轴恰有两个交点. …4分
的图象与x轴恰有两个交点. …4分
(ii)设x1,x2是方程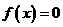 的两个实根,则
的两个实根,则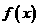 有因式
有因式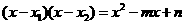 ,且可令
,且可令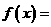
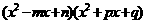 . 于是有
. 于是有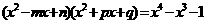 .
①
.
①
分别比较(*)式中常数项和含x3的项的系数,得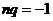 ,
,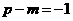 ,
,
解得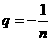 ,
, .
.
所以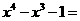
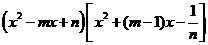 .
.
分别比较①式中含x和x2的项的系数,得
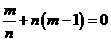 ,………②,
,………②,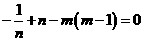 ,③
,③
②× + ③×n得
+ ③×n得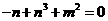 ,即
,即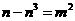 .…………10分
.…………10分
(2)方程化为: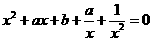 ,
,
令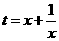 ,方程为
,方程为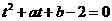 ,
,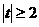 ,即有绝对值不小于2的实根.
,即有绝对值不小于2的实根.
设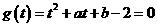
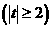 ,
,
当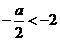 ,即
,即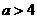 时,只需
时,只需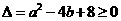 ,此时,
,此时,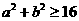 ;
;
当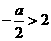 ,即
,即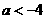 时,只需
时,只需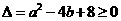 ,此时,
,此时,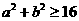 ;
;
当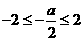 ,即
,即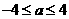 时,只需
时,只需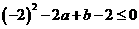 或
或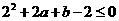 ,即
,即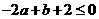 或
或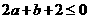 ,此时
,此时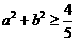 .
.
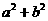 的最小值为
的最小值为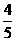 .…………………………………………………16分
.…………………………………………………16分
(附加题)
19.(本题满分16分)
设f(x)=x3,等差数列{an}中a3=7,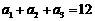 ,记Sn=
,记Sn=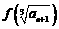 ,令bn=anSn,数列
,令bn=anSn,数列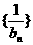 的前n项和为Tn.
的前n项和为Tn.
(1)求{an}的通项公式和Sn;
(2)求证:Tn<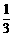 ;
;
(3)是否存在正整数m,n,且1<m<n,使得T1,Tm,Tn成等比数列?若存在,求出m,n的值,若不存在,说明理由.
解:(1)设数列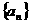 的公差为
的公差为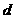 ,由
,由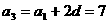 ,
,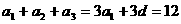 .
.
解得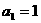 ,
,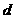 =3,∴
=3,∴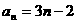 ∵
∵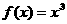
∴Sn=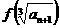 =
=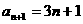 .…4分
.…4分
(2) 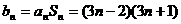 ,∴
,∴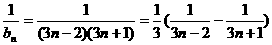
∴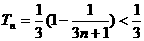 。
………………………8分
。
………………………8分
(3)由(2)知,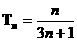 ∴
∴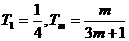 ,
,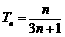
∵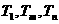 成等比数列.
成等比数列.
∴ 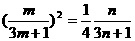 ,即
,即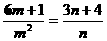 ………………………9分
………………………9分
当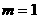 时,7
时,7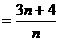 ,
,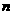 =1,不合题意;
=1,不合题意;
当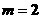 时,
时,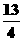
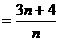 ,
,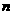 =16,符合题意;………………………10分
=16,符合题意;………………………10分
当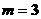 时,
时,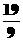
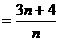 ,
,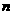 无正整数解;当
无正整数解;当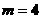 时,
时,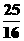
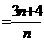 ,
,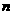 无正整数解;
无正整数解;
当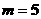 时,
时,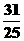
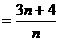 ,
,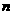 无正整数解;
无正整数解;
当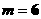 时,
时,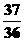
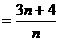 ,
,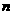 无正整数解; ………………………12分
无正整数解; ………………………12分
当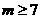 时,
时,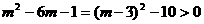 ,则
,则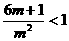 ,而
,而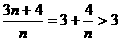 ,
,
所以,此时不存在正整数m,n,且1<m<n,使得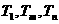 成等比数列. ………15分
成等比数列. ………15分
综上,存在正整数m=2,n=16,且1<m<n,使得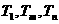 成等比数列.…………16分
成等比数列.…………16分
18.(本题满分16分)
已知曲线E:ax2+by2=1(a>0,b>0),经过点M(,0)的直线l与曲线E交
于点A、B,且→=-2→.
(1)若点B的坐标为(0,2),求曲线E的方程;
(2)若a=b=1,求直线AB的方程.
解:
(1) 设A(x0,y0),因为B(0,2),M(,0)
故→=(-,2),→=(x0-,y0). ……………………………………2分
因为→=-2→,所以(-,2)=-2(x0-,y0).
所以x0=,y0=-1.即A(,-1). ……………………………………4分
因为A,B都在曲线E上,所以解得a=1,b=.
所以曲线E的方程为x2+=1. ……………………………………6分
(2)(法一)当a=b=1时,曲线E为圆:x2+y2=1.设A(x1,y1),B(x2,y2).
因为→=-2→,所以(x2-,y2) =-2(x1-,y1),即
设线段AB的中点为T,则点T的坐标为(,),即(,-).
所以((OT=(,-),((AB=(x2-x1,y2-y1)=(-3x1,-3y1).
因为OT⊥AB,所以((OT×((AB=0,即3-4x1+3x+3y=0.
因为x+y=1,所以x1=,y1=±.
当点A的坐标为(,-)时,对应的点B的坐标为(0,1),此时直线AB的斜率
k=-,所求直线AB的方程为y=-x+1;
当点A的坐标为(,)时,对应的点B的坐标为(0,-1),此时直线AB的斜率k=,
所求直线AB的方程为y=x-1. ……………………………………16分
(法二)当a=b=1时,曲线E为圆:x2+y2=1.设A(x1,y1),B(x2,y2).
因为→=-2→,所以(x2-,y2) =-2(x1-,y1),即
因为点A,B在圆上,所以
由①×4-②,得(2x1+x2)(2x1-x2)=3.所以2x1-x2=,解得x1=,x2=0.
 由x1=,得y1=±.(以下同方法一)
由x1=,得y1=±.(以下同方法一)
(法三)如图,设AB中点为T.
则TM=TA-MA=AB,OM=.
根据Rt△OTA和Rt△OTM,得
即解得AB=,OT=.所以在Rt△OTM中,tanÐOMT==.
所以kAB=-或.所以直线AB的方程为y=-x+1或y=x-1.
17.(本题满分14分)
某公司为了加大产品的宣传力度,准备立一块广告牌,在其背面制作一个形如△ABC的支架,要求∠ACB=60°,BC的长度大于1米,且AC比AB长0.5米.为节省材料,要求AC的长度越短越好,求AC的最短长度,且当AC最短时,BC的长度为多少米?
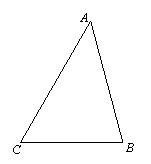 解:设BC=x米(x>1),AC=y米,则AB=y-.
解:设BC=x米(x>1),AC=y米,则AB=y-.
在△ABC中,由余弦定理,得(y-)2=y2+x2-2xycos60°.
所以y=(x>1).
法一:y==(x-1)++2≥2+.
当且仅当x-1=,即x=1+时,y有最小值2+.
法二: y′==.
由y′=0得x=1+.因为当1<x<1+时,y′<0;当x>1+时,y′>0,
所以当x=1+时,y有最小值2+.
答:AC的最短长度为2+米,此时BC的长度为(1+)米.……………14分
16.(本题满分14分)
在三棱锥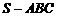 中,
中,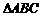 是边长为
是边长为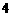 的正三角形,平面
的正三角形,平面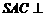 平面
平面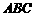 ,
,
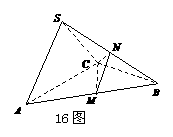
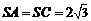 ,
,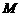 、
、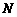 分别为
分别为 、
、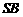 的中点.
的中点.
⑴证明: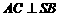 ;
;
⑵(理)求二面角 的正切值;
的正切值;
⑶求点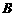 到平面
到平面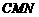 的距离.
的距离.
解:
解法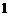 :⑴取
:⑴取 中点
中点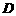 ,连结
,连结 、
、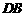 .
.
∵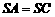 ,
,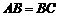 ∴
∴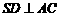 ,
,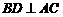 ,
,
∴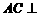 平面
平面 ,又
,又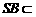 平面
平面 ,∴
,∴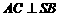 . ……4分
. ……4分
⑵∵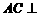 平面
平面 ,
,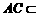 平面
平面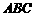 ,∴平面
,∴平面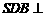 平面
平面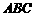 .
.
过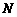 作
作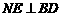 于
于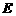 ,则
,则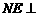 平面
平面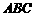 ,
,
过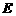 作
作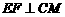 于
于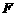 ,连结
,连结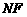 ,则
,则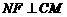 ,
,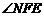 为二面角
为二面角 的平面角.
的平面角.
∵平面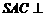 平面
平面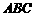 ,
,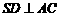 ,∴
,∴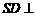 平面
平面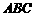 .
.
又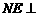 平面
平面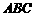 ,∴
,∴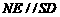 .∵
.∵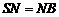 ,
,
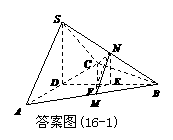 ∴
∴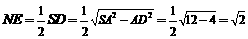 ,且
,且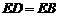 .
.
在正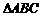 中,由平几知识可求得
中,由平几知识可求得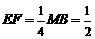 ,
,
在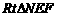 中,
中,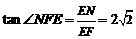
∴二面角 的正切值为
的正切值为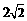 . ……8分
. ……8分
⑶在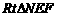 中,
中,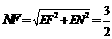 ,∴
,∴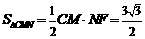 ,
,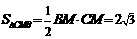 .
.
设点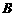 到平面
到平面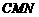 的距离为
的距离为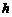 ,
,
∵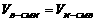 ,
,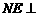 平面
平面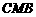 ,∴
,∴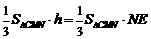 ,
,
∴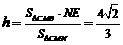 .即点
.即点 到平面
到平面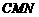 的距离为
的距离为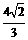 . ……14分
. ……14分
 解法
解法 :⑴取
:⑴取 中点
中点 ,连结
,连结 、
、 .∵
.∵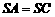 ,
,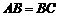 ,
,
∴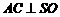 ,
,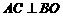 .∵平面
.∵平面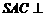 平面
平面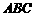 ,
,
平面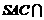 平面
平面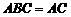 ,∴
,∴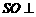 平面
平面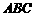 ,∴
,∴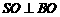 .
.
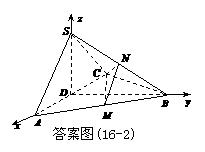
如图所示建立空间直角坐标系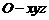 ,则
,则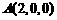 ,
,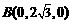 ,
,
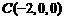 ,
,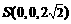 ,∴
,∴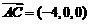 ,
,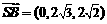 ,
,
∵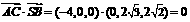 ,∴
,∴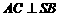 . ……6分
. ……6分
⑵∵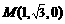 ,
,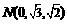 ,又
,又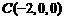 ,∴
,∴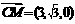 ,
,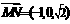 .
.
设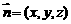 为平面
为平面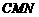 的一个法向量,则
的一个法向量,则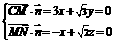 ,
,
取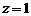 ,
,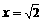 ,
,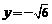 ,∴
,∴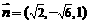 .又
.又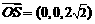 为平面
为平面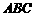 的一个法向量,
的一个法向量,
∴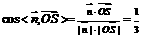 ,得
,得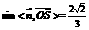
∴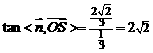 .即二面角
.即二面角 的正切值为
的正切值为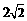 . ……10分
. ……10分
⑶由⑴⑵得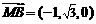 ,又
,又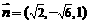 为平面
为平面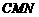 的一个法向量,
的一个法向量,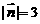 ,
,
∴点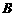 到平面
到平面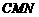 的距离
的距离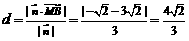 .……14分
.……14分
15.(本题满分14分)
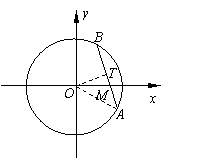
 如图所示,已知
如图所示,已知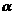 的终边所在直线上的一点
的终边所在直线上的一点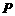 的坐标为
的坐标为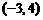 ,
,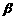 的终边在第一象限且与单位圆的交点
的终边在第一象限且与单位圆的交点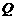 的纵坐标为
的纵坐标为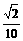 .
.
⑴求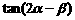 的值;
的值;
⑵若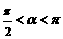 ,
,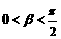 ,求
,求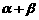 .
.
解:⑴由三角函数的定义知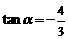
∴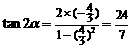 .
.
又由三角函数线知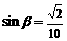 ,
,
∵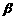 为第一象限角,∴
为第一象限角,∴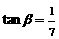 ,∴
,∴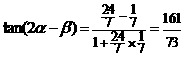 .
……7分
.
……7分
⑵∵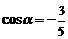 ,
,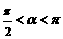 ,∴
,∴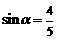 .
.
又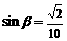 ,
,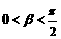 ,∴
,∴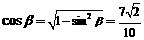 . …8分
. …8分
∴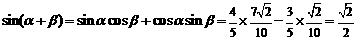 .
.
由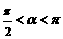 ,
,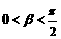 ,得
,得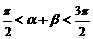 ,∴
,∴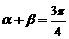 .
……14分
.
……14分
14.已知定义在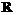 上的函数f(x)满足f(1)=2,
上的函数f(x)满足f(1)=2,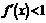 ,则不等式
,则不等式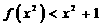 解集
解集
▲ .
答案: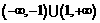 二、解答题:本大题共6小题,共计90分.请把答案写在答题卡相应的位置上.解答时应写出文字说明,证明过程或演算步骤.
二、解答题:本大题共6小题,共计90分.请把答案写在答题卡相应的位置上.解答时应写出文字说明,证明过程或演算步骤.
13.已知a > 0,b > 0,且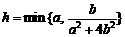 ,其中
,其中 {a,b}表示数a,b中较小的数,则h的最大值为 ▲ .
{a,b}表示数a,b中较小的数,则h的最大值为 ▲ .
答案: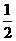
12.已知等差数列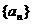 的公差d不为0,等比数列
的公差d不为0,等比数列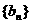 的公比q为小于1的正有理数。若
的公比q为小于1的正有理数。若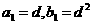 ,且
,且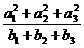 是正整数,则q等于 ▲ .
是正整数,则q等于 ▲ .
答案: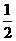
11.已知A,B,P是双曲线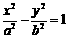 上不同的三点,且A,B连线经过坐标原点,若直线
上不同的三点,且A,B连线经过坐标原点,若直线
PA,PB的斜率乘积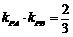 ,则该双曲线的离心率为 ▲ .
,则该双曲线的离心率为 ▲ .
答案: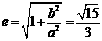
解析: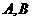 一定关于原点对称,设
一定关于原点对称,设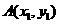 ,
,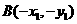 ,
,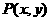
则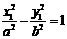 ,
,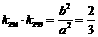 ,
,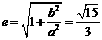 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com