
题目列表(包括答案和解析)
20.(本小题满分14分)
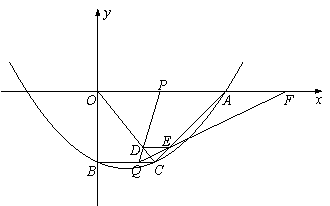
如图,在平面直角坐标系xoy中,抛物线y=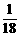 x 2-
x 2-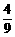 x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
(1)求A,B,C三点的坐标和抛物线的顶点坐标;
(2)当t为何值时,四边形PQCA为平行四边形?请写出计算过程;
(3)当t∈(0,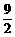 )时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;
)时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;
 (4)当t为何值时,△PQF为等腰三角形?请写出解答过程.
(4)当t为何值时,△PQF为等腰三角形?请写出解答过程.
19.(本小题满分14分)
 如图,有一正方形钢板
如图,有一正方形钢板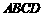 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线 是以直线AD为对称轴,以线段
是以直线AD为对称轴,以线段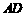 的中点
的中点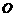 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线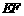 ,可使剩余的直角梯形的面积最大?并求其最大值.
,可使剩余的直角梯形的面积最大?并求其最大值.
18.(本小题满分12分)

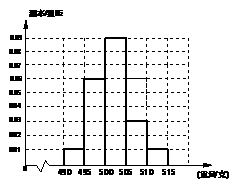 某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在
某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在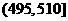 的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
表1:(甲流水线样本频数分布表) 图1:(乙流水线样本频率分布直方图)
(1)根据上表数据在答题卡上作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从乙流水线上任取5件产品,恰有3件产品为合格品的概率;
(3)由以上统计数据完成下面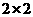 列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关” .
列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关” .
|
|
甲流水线 |
乙流水线 |
合计 |
|
合格品 |
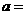 |
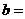 |
|
|
不合格品 |
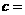 |
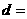 |
|
|
合 计 |
|
|
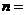 |
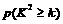 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
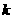 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
附:下面的临界值表供参考:
(参考公式: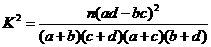 ,其中
,其中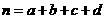 )
)
17.(本小题满分14分)
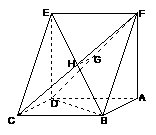 已知如图:平行四边形ABCD中,
已知如图:平行四边形ABCD中,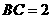 , BD⊥CD,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
, BD⊥CD,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
(1)求证:GH∥平面CDE;
(2)记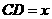 ,
,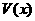 表示四棱锥F-ABCD体积,
表示四棱锥F-ABCD体积,
求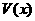 的表达式;
的表达式;
(3)当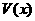 取得最大值时,求平面ECF与平面ABCD
取得最大值时,求平面ECF与平面ABCD
所成的二面角的正弦值.
16.(本小题满分12分)
设函数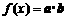 ,其中向量
,其中向量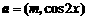 ,
,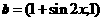 ,
,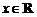 ,且
,且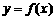 的图象经过点
的图象经过点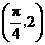 .
.
(Ⅰ)求实数 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数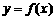 的对称中心。(Ⅲ)求函数
的对称中心。(Ⅲ)求函数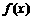 的最小值及此时
的最小值及此时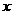 值的集合.
值的集合.
15.(坐标系与参数方程选做题) 已知直线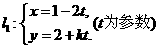 ,
,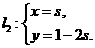
(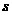 为参数),若
为参数),若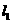 //
//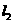 ,则
,则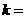 ;若
;若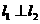 ,则
,则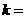 .
.
14.(几何证明选做题)如图所示,圆的内接三角形ABC的角平分
线BD与AC交于点D,与圆交于点E,连结AE,已知ED=3,
BD=6 ,则线段AE的长= .
13. 已知函数
已知函数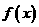 满足:
满足: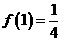 ,
,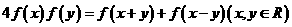 ,则
,则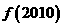 =_____________.
=_____________.
12.已知双曲线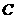 :
: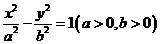 的离心率
的离心率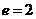 ,且它的一个顶点到较近焦点的距离为
,且它的一个顶点到较近焦点的距离为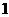 ,则双曲线
,则双曲线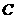 的方程为
的方程为
11.点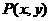 在不等式组
在不等式组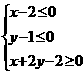 表示的平面区域上运动,则
表示的平面区域上运动,则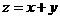 的最大值为 ___
的最大值为 ___
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com