1．了解空间两条直线的位置关系．

3．(习题三第7题)已知两条直线：

l1：(3+m)x+4y=5-3m，

l2：2x+(5+m)y=8．

m为何值时，l1与l2：(1)相交；(2)平行；(3)重合．

解：(1)m≠1且m≠-7；(2)m=-7；(3)m=-1．

2．(教材第35页，1．9练习第3题)A和C取什么值时，直线Ax-2y-1=0和直线6x-4y+c=0(1)平行；(2)重合；(3)相交．

解：(1)A=3，C≠-2；(2)A=3，C=-2；(3)A≠3．

1．(教材第35页，1．9练习第2题)判断下列各对直线的位置关系，如果相交，则求出交点的坐标：

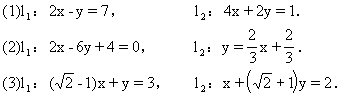
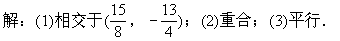
(五)课后小结

(1)两直线的位置关系与它们对应的方程的解的个数的对应关系．

(2)直线的三种位置关系所对应的方程特征．

(3)对方程组中系数含有字母的两直线位置关系的讨论方法．

(四)例题

例1　 求下列两条直线的交点：

l1：3x+4y-2=0，　 l2：　 2x+y+2=0．

解：解方程组

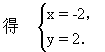
∴l1与l2的交点是M(-2，2)．

例2　 已知两条直线：

l1：　 x+my+6=0，

l2：　 (m-2)x+3y+2m=0．

当m为何值时，l1与l2：(1)相交，(2)平行，(3)重合．

解：将两直线的方程组成方程组

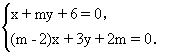
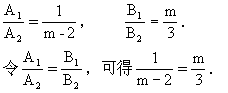
解得m=-1或m=3．

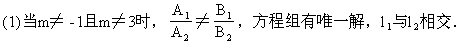
(2)当m=-1时，方程组为

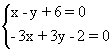
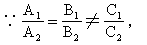
∴方程无解，l1与l2平行．

(3)当m=3时，方程组为

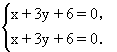
两方程为同一个方程，l1与l2重合．

(三)统一通过解方程组研究两直线的位置关系与通过斜率研究两直线位置关系的结论

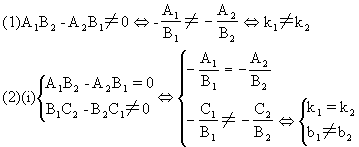
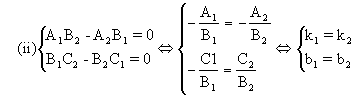
说明：在平面几何中，我们研究两直线的位置关系时，不考虑两条直线重合的情况，而在解析几何中，由于两个不同的方程可以表示同一条直线，我们把重合也作为两直线的一种位置关系来研究．

(二)对方程组的解的讨论

若A1、A2、B1、B2中有一个或两个为零，则两直线中至少有一条与坐标轴平行，很容易得到两直线的位置关系．

下面设A1、A2、B1、B2全不为零．

解这个方程组：

(1)×B2得　 A1B2x+B1B2y+B2C1=0，　　　　　　　　　　 (3)

(2)×B1得　 A2B1x+B1B2y+B1C2=0．　　　　　　　　　　 (4)

(3)-(4)得(A1B2-A2B1)x+B2C1-B1C2=0．

下面分两种情况讨论：

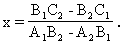
将上面表达式中右边的A1、A2分别用B1、B2代入即可得

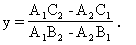
上面得到y可把方程组写成

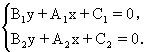
即将x用y换，A1、A2分别与B1、B2对换后上面的方程组还原成原方程组．

综上所述，方程组有唯一解：

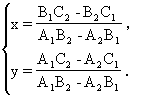
这时l1与l2相交，上面x和y的值就是交点的坐标．

(2)当A1B2-A2B1=0时：

①当B1C2-B2C1≠0时，这时C1、C2不能全为零(为什么？)．设C2

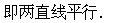
②如果B1C2-B2C1=0，这时C1、C2或全为零或全不为零(当C1、

(一)两直线交点与方程组解的关系

设两直线的方程是

l1：　 A1x+B1y+c1=0，　 l2：　 A2x+B2y+C2=0．

如果两条直线相交，由于交点同时在两条直线上，交点的坐标一定是这两个方程的公共解；反之，如果这两个二元一次方程只有一个公共解，那么以这个解为坐标的点必是直线l1和l2的交点．因此，两条直线是否相交，就要看这两条直线的方程所组成的方程组

是否有唯一解．

分析、启发、诱导、讲练结合．