
题目列表(包括答案和解析)
9.已知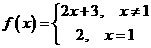 ,下面结论正确的是( )
,下面结论正确的是( )
A.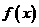 在
在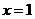 处连续 B.
处连续 B.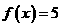 C.
C.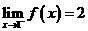 D.
D.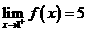
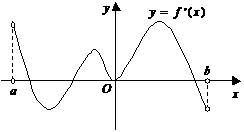
8.函数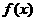 的定义域为开区间
的定义域为开区间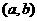 ,导函数
,导函数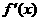 在
在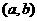 内的图象如图所示,则函数
内的图象如图所示,则函数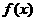 在开区间
在开区间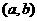 内有极小值点( )
内有极小值点( )
A.1个
B.2个
C.3个
D. 4个
7. 设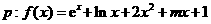 在
在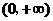 内单调递增,
内单调递增,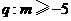 ,则
,则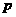 是
是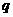 的( )
的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
6.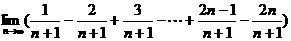 的值为( ).
的值为( ).
A.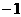 B.0
C.
B.0
C.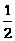 D.1
D.1
5.函数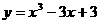 在
在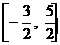 上的最小值是 ( )
上的最小值是 ( )
A. 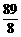 B. 1 C.
B. 1 C. 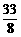 D. 5
D. 5
4.已知函数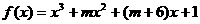 既存在极大值又存在最小值,则实数m的取值范围是( ).
既存在极大值又存在最小值,则实数m的取值范围是( ).
A
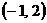 B.
B.
C.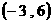 D.
D. 
3.下列函数在x =0处连续的是( ).
A.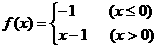 B.
B.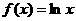
C.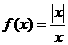 D.
D.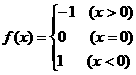
2.已知对任意实数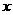 ,有
,有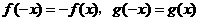 ,且
,且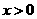 时,
时,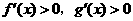 ,则
,则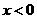 ( )
( )
A.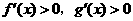 B.
B.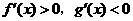
C.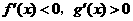 D.
D.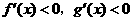
函数极限和数列极限仍然以选择或填空题为主,有时会在解答题的最后一问出现难度中等或偏易。(文科生对函数极限不做要求)
导数的考查方式以客观题为主,主要考查求导数的基本公式和法则,以及导数的几何意义。也可以解答题的形式出现,即以导数的几何意义为背景设置成导数与解析几何的综合题。导数的应用是重点,侧重于利用导数确定函数的单调性和极值、最值、值域问题,侧重于导数的综合应用,即导数与函数、数列、不等式的综合应用。
4 强化训练
(要求选择填空解答兼有并留有解答空间,便于用户直接应用)
1 选择题
1.已知曲线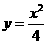 的一条切线的斜率为
的一条切线的斜率为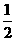 ,则切点的横坐标为( )
,则切点的横坐标为( )
A.1 B.2 C.3 D.4
2.导数是中学限选内容中较为重要的知识,由于其应用的广泛性,为我们解决所学过的有关函数问题提供了一般性方法,是解决实际问题强有力的工具。导数的概念及其运算是导数应用的基础,是高考重点考查的对象。要牢记导数公式,熟练应用导数公式求函数的导数,掌握求导数的方法。应用导数解决实际问题的关键是要建立恰当的数学模型,了解导数概念的实际背景。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com