
题目列表(包括答案和解析)
4.若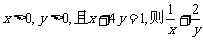 的最小值为 ( )
的最小值为 ( )
A.9 B.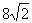 C.
C.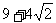 D.
D.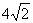
3.已知向量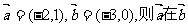 方向上的投影为 ( )
方向上的投影为 ( )
A.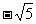 B.
B.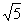 C.-2 D.2
C.-2 D.2
2.已知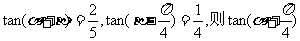 等于 ( )
等于 ( )
A.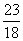 B.
B.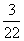 C.
C.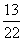 D.
D.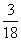
1.已知集合 的真子集,则实数a的取值个数是 ( )
的真子集,则实数a的取值个数是 ( )
A.0个 B.1个 C.3个 D.无数个
21.解:(1)由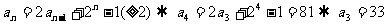
同理可得 a2 = 13, a1 = 5. 3分
(2)假设存在的实数λ符合题意,则
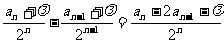
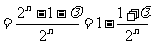 必是与n无关的常数,则
必是与n无关的常数,则
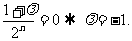 7分
7分
故存在实数λ=-1,使得数列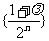 为等差数列.
为等差数列.
(3)由(2)知数列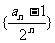 是公差d = 1的等差数列
是公差d = 1的等差数列
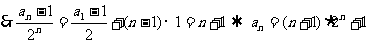 9分
9分
Sn = n+2×2 + 3×22 + 4×23 +…+(n+1)·2n+1
2Sn = 2n+2×22 + 3×22 +…+n·2n + (n+1)·2n+1
 相减整理得: Sn =
n(2n+1
+1)
12分
相减整理得: Sn =
n(2n+1
+1)
12分
22解:(1)设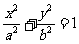 ,则
,则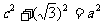 ,
,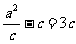 ,
,
解得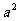 =4,c=1,所以椭圆方程为
=4,c=1,所以椭圆方程为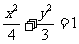 。……………4分
。……………4分
(2)设PQ的方程为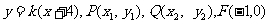
因为PF⊥QF,所以 ,
,
即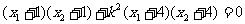 ,
,
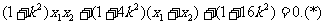 ……………8分
……………8分
联立得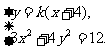
消去y,得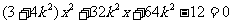 ,……………10分
,……………10分
由 ,得
,得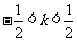 ……………11分
……………11分
所以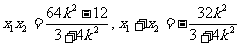 .……………12分
.……………12分
代入(*)式化简,得8k2=1,所以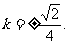
则直线PQ的方程为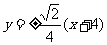 .……………14分
.……………14分
20.解:(1)由题意可得,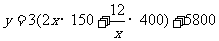
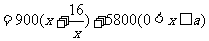 ………………5分
………………5分
(2)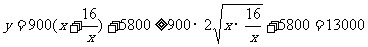
当且仅当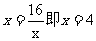 时取等号……………………7分
时取等号……………………7分
若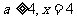 时,有最小值13000.………………8分
时,有最小值13000.………………8分
若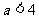 ,任取
,任取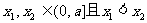
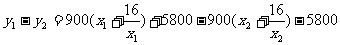
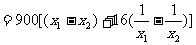
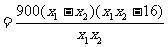
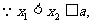
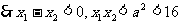
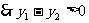
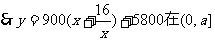 上是减函数………………10分
上是减函数………………10分
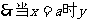 有最小值
有最小值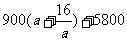 ………………12分
………………12分
(此题利用导数相应得分)
19.由三视图知,该多面体是底面为直角三角形的直三棱柱ADE-BCF,且AB=BC=BF=2,DE=CF=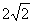 ,∠CBF=
,∠CBF=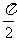
①证明:取BF的中点G,连结MG、NG,由M、N分别为AF、BC中点,可得,NG∥CF,MG∥EF
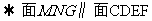
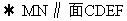 ……6分
……6分
②取DE中点为H,因为AD=AE
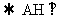 DE
DE
在直三棱柱AED-BCF中
平面ADE⊥平面CDEF
面ADE∩面CDEF=DE
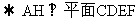
 多面体A-CDEF是以AH为高,以矩形CDEF为底面的棱锥
多面体A-CDEF是以AH为高,以矩形CDEF为底面的棱锥
在△ADE中,AH=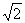
S矩形CDEF=DE·EF=4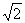
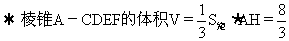 ……12分
……12分
18.解:(I)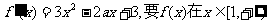 上是增函数,则有
上是增函数,则有
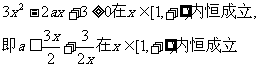
又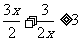 (当且仅当x=1时取等号),所以a≤3………6分
(当且仅当x=1时取等号),所以a≤3………6分
(II)由题意知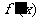 =3x2-2ax+3=0的一个根为x=3,可得a=5,
=3x2-2ax+3=0的一个根为x=3,可得a=5,
所以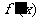 =3x2-10x+3=0的根为x=3或x=
=3x2-10x+3=0的根为x=3或x=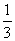 (舍去),又f(1)=-1,
(舍去),又f(1)=-1,
f(3)=-9,f(5)=15,
∴f(x)在x∈[1,5]上的最小值是f(3)=-9,最大值是f(5)=15……12分
17.
解: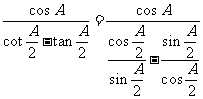
=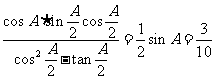
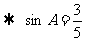 ………………6分
………………6分
a2>b2+c2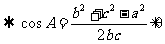
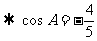 ………………10分
………………10分
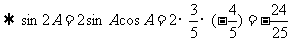 ………………12分
………………12分
21.
已知数列{an}满足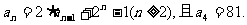
(1)求数列的前三项:a1,a2,a3;
(2)是否存在一个实数λ,使得数列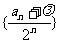 为等差数列?若存在,求出λ的值;若不存在,说明理由;
为等差数列?若存在,求出λ的值;若不存在,说明理由;
(3)求数列{an}的前n项和Sn.
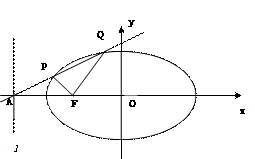 22椭圆的中心在原点O,短轴长为
22椭圆的中心在原点O,短轴长为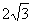 ,左焦点为
,左焦点为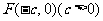 ,直线
,直线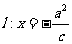 与
与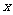 轴交于点A,且
轴交于点A,且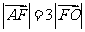 ,过点A的直线与椭圆相交于P,Q两点.
,过点A的直线与椭圆相交于P,Q两点.
(1)求椭圆的方程.
(2)若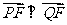 ,求直线PQ的方程.
,求直线PQ的方程.
BDACA DBDCC DC
充分不必要 -15 4 ③
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com