
∴∠O1FO是二面角O1-BC-D的平面角,………………3分
试题详情
∵OB=2,∠OBF=60°,∴OF= . . 试题详情
在Rt△O1OF在,tan∠O1FO= ∴∠O1FO=60° 即二面角O1―BC―D为60°………………6分 (2)在△O1AC中,OE是△O1AC的中位线,∴OE∥O1C ∴OE∥O1BC,∵BC⊥面O1OF,∴面O1BC⊥面O1OF,交线O1F. 过O作OH⊥O1F于H,则OH是点O到面O1BC的距离,………………10分 试题详情

解法二:(1)∵OO1⊥平面AC, ∴OO1⊥OA,OO1⊥OB,又OA⊥OB,………………2分 建立如图所示的空间直角坐标系(如图) ∵底面ABCD是边长为4,∠DAB=60°的菱形,
试题详情
∴OA=2 ,OB=2, ,OB=2, 试题详情
则A(2 ,0,0),B(0,2,0),C(-2 ,0,0),B(0,2,0),C(-2 ,0,0),O1(0,0,3)………………3分 ,0,0),O1(0,0,3)………………3分 试题详情
设平面O1BC的法向量为 =(x,y,z), =(x,y,z), 试题详情
试题详情
∴ ,则z=2,则x=- ,则z=2,则x=- ,y=3, ,y=3, 试题详情
试题详情
试题详情
设O1-BC-D的平面角为α, ∴cosα= ∴α=60°. ∴α=60°. 故二面角O1-BC-D为60°. ………………6分 (2)设点E到平面O1BC的距离为d, 试题详情
试题详情
则d= ∴点E到面O1BC的距离等于 ∴点E到面O1BC的距离等于 。……………12分 。……………12分 试题详情
试题详情
(1)证明 。 。 试题详情
(2)求侧面 与底面 与底面 所成二面角的大小。 所成二面角的大小。 (3)求异面直线SC与AB所成角的大小。 解:(1)∵∠SAB=∠SCA=900 试题详情
试题详情
(2) 试题详情
试题详情
(3) 试题详情
试题详情
试题详情
3、(江苏省启东中学高三综合测试二)在Rt△ABC中,∠ACB=30°,∠B=90°,D为AC中点,E为BD的中点,AE的延长线交 BC于F,将△ABD沿BD折起,二面角A-BD-C大小记为θ. 试题详情
 (Ⅰ)求证:面AEF⊥面BCD; (Ⅰ)求证:面AEF⊥面BCD;
(Ⅱ)θ为何值时,AB⊥CD. 解:(Ⅰ)证明:在Rt△ABC中,∠C=30°,D为AC的中点,则△ABD是等边三角形 又E是BD的中点,∵BD⊥AE,BD⊥EF,折起后,AE∩EF=E,∴BD⊥面AEF 试题详情
∵BD 面BCD,∴面AEF⊥面BCD 面BCD,∴面AEF⊥面BCD (Ⅱ)解:过A作AP⊥面BCD于P,则P在FE的延长线上,设BP与CD相交于Q, 令AB=1,则△ABD是边长为1的等边三角形,若AB⊥CD,则BQ⊥CD 试题详情

由于∠AEF=θ就是二面角A-BD-C的平面角, 试题详情
试题详情
4、(江苏省启东中学高三综合测试三) 如图,在斜三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成60°的角,AA1=2,底面ABC是边长为2的正三角形,其重心为G点,E是线段BC1上一点,且BE= 如图,在斜三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成60°的角,AA1=2,底面ABC是边长为2的正三角形,其重心为G点,E是线段BC1上一点,且BE= BC1。 BC1。 (1)求证:GE∥侧面AA1B1B; (2)求平面B1GE与底面民ABC所成锐二面角的大小。 试题详情
答案:(1)略;(2)arctan (arccos (arccos ) ) 试题详情
 5、(江苏省启东中学高三综合测试四)如图, 正方形ABCD和ABEF的边长均为1,且它们所在的平面互相垂直,G为BC的中点. 5、(江苏省启东中学高三综合测试四)如图, 正方形ABCD和ABEF的边长均为1,且它们所在的平面互相垂直,G为BC的中点.
(Ⅰ)求点G到平面ADE的距离; 试题详情
(Ⅱ)求二面角 的正切值. 的正切值. 试题详情
解:(Ⅰ)∵BC∥AD,
AD 面ADE, 面ADE, ∴点G到平面ADE的距离即点B到平面ADE的距离. 连BF交AE于H,则BF⊥AE,又BF⊥AD. 试题详情
 ∴BH即点B到平面ADE的距离. ∴BH即点B到平面ADE的距离.
试题详情
在Rt△ABE中, . . 试题详情
∴点G到平面ADE的距离为 . . (Ⅱ)过点B作BN⊥DG于点N,连EN, 由三垂线定理知EN⊥DN. 试题详情
∴ 为二面角 为二面角 的平面角. 的平面角. 试题详情
在Rt△BNG中, 试题详情
∴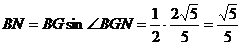 试题详情
则Rt△EBN中, 试题详情
所以二面角 的正切值为 的正切值为 . . 试题详情
试题详情
 ; ;
试题详情
试题详情
(2)求由面 与面 与面 所成角的二面角的正切 所成角的二面角的正切 解:(1)M为PC的中点,设PD中点为N, 试题详情
 则MN= 则MN= CD,且MN// CD,且MN// CD,∴MN=AB,MN//AB CD,∴MN=AB,MN//AB
∴ABMN为平行四边形,∴BM//AN, 又PA=AD,∠PAD=900 ∴AN⊥PD, 又CD⊥AN,∴AN⊥面PCD,∴BM⊥面PCD, (1) 延长CB交DA于E, 试题详情
∵AB= CD。AB// CD。AB// CD CD ∴AE=AD=PA,∴PD⊥PE 又∴PE⊥CD,∴PE⊥面PCD, 试题详情
∴∠CPD为二面角C-PE-D的平面角;PD= AD,CD=2AD; AD,CD=2AD; 试题详情
 ∴tan∠CPD= ∴tan∠CPD=
试题详情
试题详情
(I)求证: 平面 平面 ; ; 试题详情
(II)求 到平面 到平面 的距离; 的距离; 试题详情
(III)求二面角 的大小。 的大小。 试题详情
解:(I)因为 平面 平面 , , 试题详情
所以平面 平面 平面 , , 试题详情
试题详情
得 ,又 ,又 试题详情
所以 平面 平面 ;……………4分 ;……………4分 试题详情
(II)因为 ,所以四边形 ,所以四边形 为 为 菱形, 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
从而 为二面角 为二面角 的平面角, 的平面角, 试题详情
试题详情
在 中, 中, , , 试题详情
故二面角 的大小为 的大小为 。……………12分 。……………12分 试题详情
试题详情
试题详情
以 为 为 轴建立空间坐标系, 轴建立空间坐标系, 试题详情
试题详情
 , , , ,
试题详情
 , , , ,
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
故  ,根据法向量的方向, ,根据法向量的方向, 试题详情
可知二面角 的大小为 的大小为 。 。 试题详情
8、(四川省成都市新都一中高2008级一诊适应性测试)如图,直三棱柱ABC―A1B1C1中,AB=AC=AA1=a,且∠CAB=90°,三棱锥P-ABC中,P∈平面BB1C1C,且PB=PC=. (1)求直线PA 与平面ABC所成角的正切值 (2)求证:PB//平面AB1C (3)求二面角A-PB-C的大小. 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
9、 (四川省成都市一诊)如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=BC=2,E为PA的中点,过E作平行于底面的平面EFGH,分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形,AD∥BC,AB⊥AD,∠BCD=135°. (四川省成都市一诊)如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=BC=2,E为PA的中点,过E作平行于底面的平面EFGH,分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形,AD∥BC,AB⊥AD,∠BCD=135°. (1) 求异面直线AF与BG所成的角的大小; (2) 求平面APB与平面CPD所成的锐二面角的大小. 试题详情
 解:由题意可知:AP、AD、AB两两垂直,可建立空间直角坐标系A-xyz 解:由题意可知:AP、AD、AB两两垂直,可建立空间直角坐标系A-xyz
由平面几何知识知:AD=4,D(0,4,0),B(2,0,0),
C(2,2,0),P(0,0,2),E(0,0,1),F(1,0,1),G(1,1,1) ……2分
(1)=(1,0,1),=(-1,1,1)
∴?=0
∴AF与BG所成角为
……4分
(2)可证明AD⊥平面APB
∴平面APB的法向量为n=(0,1,0)
设平面CPD的法向量为m=(1,y,z)
由 Þ Þ
故m=(1,1,2)
∵cos<m,n>=
∴平面APB与平面CPD所成的锐二面角的大小为arccos
试题详情
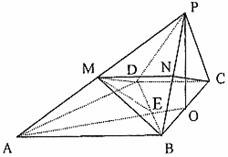
10、(四川省成都市新都一中高2008级12月月考)如图,已知四棱锥P―ABCD的底面是直角梯形,∠ABC=∠BCD=90°, 试题详情
 AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC中点,AO交BD于E. AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC中点,AO交BD于E.
(1)求证:PA⊥BD; (2)求二面角P-DC-B的大小; (3)求证:平面PAD⊥平面PAB. 本题考查空间直线与平面、平面与平面的位置关系,二面角, 空间想想能力,以及综合解题能力 试题详情
方法一:(1)证明: 试题详情
又 平面 平面 平面ABCD 平面ABCD 试题详情
平面 平面ABCD=BC, 平面ABCD=BC, 平面ABCD ……2分 平面ABCD ……2分 试题详情
在梯形ABCD中,可得 试题详情
 ,即 ,即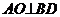 试题详情
 在平面ABCD内的射影为AO, 在平面ABCD内的射影为AO, ……4分 ……4分 试题详情
(2)解: ,且平面 ,且平面 平面ABCD 平面ABCD 试题详情
∴DC⊥平面PBC  平面PBC, 平面PBC,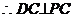 ∴∠PCB为二面角P―DC―B的平面角 ……6分 ∵△PBC是等边三角形,∴∠PCB=60°,即二面角P―DC―B的大小为60° ……8分 试题详情
∵PC=BC,∴CN⊥PB
①
试题详情
 ,且平面 ,且平面 平面ABCD 平面ABCD 试题详情
 平面PBC ……………10分 平面PBC ……………10分 试题详情
 平面PAB 平面PAB  平面 平面 平面PAB ② 平面PAB ② 由①、②知CN⊥平面PAB 连结DM、MN,则由MN∥AB∥CD MN=AB=CD,得四边形MNCD为平行四边形 ∴CN∥DM 试题详情
|
试题详情
∵DMÌ平面PAD  平面PAD⊥平面PAB ………………12分 平面PAD⊥平面PAB ………………12分 方法二:取BC的中点O,因为△PBC是等边三角形, 由侧面PBC⊥底面ABCD 得PO⊥底面ABCD ……1分 以BC中点O为原点,以BC所在直线为x轴,过点O与 AB平行的直线为y轴,建立如图所示的空间直角坐标系 O―xyz……2分 试题详情
(1)证明:∵CD=1,则在直角梯形中, 试题详情
在等边三角形PBC中, 试题详情
试题详情
试题详情
试题详情
(2)解:取PC中点N,则 试题详情
试题详情
试题详情
 所夹角等于所求二面角的平面角 ……6分 所夹角等于所求二面角的平面角 ……6分 试题详情
试题详情
试题详情
(3)证明:取PA的中点M,连结DM,则M的坐标为 试题详情
又 ……10分 ……10分 试题详情
试题详情
 即 即 试题详情
试题详情
11、 (安徽省淮南市2008届高三第一次模拟考试)如图,正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧面BB1C1C所成的角为45°. (安徽省淮南市2008届高三第一次模拟考试)如图,正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧面BB1C1C所成的角为45°. (1)求此正三棱柱的侧棱长; (2)求二面角A-BD-C的大小; (3)求点C到平面ABD的距离. 试题详情
试题详情
试题详情
试题详情
 侧面 侧面 . .
试题详情
试题详情
为 . . 试题详情
试题详情
 此正三棱柱的侧棱长为 此正三棱柱的侧棱长为 .
……………………5分 .
……………………5分
注:也可用向量法求侧棱长. 试题详情
试题详情
试题详情
 为二面角 为二面角 的平面角. 的平面角.
试题详情
在 中, 中, ,又 ,又 试题详情
试题详情
又 试题详情
试题详情
故二面角 的大小为 的大小为 .
…………………………10分 .
…………………………10分 解法2:(向量法,见后) 试题详情
试题详情
在 中, 中, . .
试题详情
试题详情
试题详情
解法3:(思路)等体积变换:由 可求. 可求. 解法4:(向量法,见后) 题(Ⅱ)、(Ⅲ)的向量解法: 试题详情
(Ⅱ)解法2:如图,建立空间直角坐标系 . . 试题详情
 则 则 . .
试题详情
试题详情
试题详情
 取 取
试题详情
又平面 的一个法向量 的一个法向量
试题详情
  . .
试题详情
结合图形可知,二面角 的大小为 的大小为 .
…………10分 .
…………10分 试题详情
(Ⅲ)解法4:由(Ⅱ)解法2,  试题详情
试题详情
试题详情
(Ⅰ)求证: ∥平面 ∥平面 ; ; 试题详情
试题详情
(Ⅲ) 当 取何值时, 取何值时, 在平面 在平面 内的射影恰好为 内的射影恰好为 的重心? 的重心?
解法一:(Ⅰ)过P作MN∥B1C1,分别交A1B1、D1C1于M、N,则M、N分别为 A1B1、D1C1的中点,连MB、NC,则四边形BCNM是平行四边形 …………… 2分 试题详情
 ∵E、M分别为AB、A1B1中点,∴A1E∥MB ∵E、M分别为AB、A1B1中点,∴A1E∥MB
试题详情
又MB 平面PBC,∴A1E∥平面PBC。………… 4分 平面PBC,∴A1E∥平面PBC。………… 4分 (Ⅱ) 过A作AF⊥MB,垂足为F,连PF, 试题详情
∵BC⊥平面ABB1A1,AF 平面ABB1A1, 平面ABB1A1, ∴AF⊥BC, BC∩MB=B,∴AF⊥平面PBC, ∴∠APF就是直线AP与平面PBC所成的角,…… 7分 试题详情
试题详情
sin∠APF= 。所以,直线AP与平面PBC所成的角是 。所以,直线AP与平面PBC所成的角是 。 ………… 9分 。 ………… 9分 试题详情
(Ⅲ)连OP、OB、OC,则OP⊥BC,由三垂线定理易得OB⊥PC,OC⊥PB,所以O在平面PBC中的射影是△PBC的垂心,又O在平面PBC中的射影是△PBC的重心,则△PBC为正三角形。即PB=PC=BC,所以 。 。 试题详情
反之,当k= 时,PA=AB=PB=PC=BC,所以三棱锥 时,PA=AB=PB=PC=BC,所以三棱锥 为正三棱锥, 为正三棱锥, 试题详情
∴O在平面PBC内的射影为 的重心 的重心 ………… 13分
………… 13分 试题详情
试题详情
(Ⅰ)由上得 、 、 、 、 试题详情
 ,设 ,设 得 得
试题详情
试题详情
解得 ,
∴ ,
∴ 试题详情
 , , ∴ ∴ ∥平面 ∥平面 ………………4分
………………4分
|
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
13、(北京市朝阳区2008年高三数学一模)直三棱柱ABC-A1B1C1中,∠ACB=120°,AC=CB=A1A=1,D1是A1B1上一动点(可 试题详情
 以与A1或B1重合),过D1和C1C的平面与AB交于D. 以与A1或B1重合),过D1和C1C的平面与AB交于D.
(Ⅰ)证明BC∥平面AB1C1; (Ⅱ)若D1为A1B1的中点,求三棱 试题详情
锥B1-C1AD1的体积 ; ; (Ⅲ)求二面角D1-AC1-C的取值范围. 方法1: 试题详情
 (Ⅰ)证明:依条件有CB∥C1B1, (Ⅰ)证明:依条件有CB∥C1B1,
试题详情
又C1B1 平面A B1C1, 平面A B1C1, 试题详情
CB 平面A B1C1, 平面A B1C1, 所以CB∥平面A B1C1.…………………3分 (Ⅱ)解: 因为D为AB的中点, 依条件可知C1D⊥A1B1. 试题详情
所以 = = 试题详情
= ×C1D1×( ×C1D1×( ×A1A×D1B1) ×A1A×D1B1) 试题详情
=  × × ×( ×( ×1× ×1× )= )= .………………………………………………………7分 .………………………………………………………7分 (Ⅲ)解: 因为D1是A1B1上一动点, 所以当D1与A1重合时,二面角D1- 试题详情
 AC1-C的大小为π; ……………………………………………………………9分 AC1-C的大小为π; ……………………………………………………………9分
当D1与B1重合时, 如图,分别延长A1C1和AC1, 过B1作B1E⊥A1C1延长于E, 依条件可知平面A1B1C1⊥平面 ACC1A1, 所以B1E⊥平面ACC1A1. 过点E作EF⊥A1C1,垂直为F. 连结FB1, 所以FB1⊥A1C1. 所以∠B1FE是所求二面角的平面角. ……………………………………………11分 试题详情
容易求出B1E= ,FE= ,FE= . . 试题详情
所以tan∠B1FE= = = . . 试题详情
所以∠B1FE= arctan . (或arccos . (或arccos ) ) 试题详情
所以二面角D1-AC1-C的取值范围是[arctan ,π](或[arccos ,π](或[arccos ,π]).……13分 ,π]).……13分 试题详情
 方法2: 方法2:
(Ⅰ),(Ⅱ)略 (Ⅲ)解: 如图建立空间直角坐标系,则有 试题详情
A(1,0,0),B1(- , , ,1), ,1), C1(0,0,1). 因为D1是A1B1上一动点, 所以当D1与A1重合时,二面角 D1-AC1-C的大小为π;……………………………………………………………9分 当D1与B1重合时, 显然向量n1=(0,1,0)是平面A CC1A1的一个法向量. 试题详情
因为 =(1,0,-1), =(1,0,-1), 试题详情
 =(- =(- , , ,1), ,1), 设平面C1AB1的法向量是n2=(x,y,z), 试题详情
试题详情
因为n1?n2= ,| n1|=1,| n2|= ,| n1|=1,| n2|= , , 设二面角B1-AC1-C的大小为β, 试题详情
所以cosβ= . . 试题详情
即β=arccos . . 试题详情
所以二面角D1-AC1-C的取值范围是[arccos ,π](或[arctan ,π](或[arctan ,π]). ,π]). 试题详情
14、(北京市崇文区2008年高三统一练习一)如图,在直三棱柱ABC―A1B1C1中,∠ABC=90°,AB=BC=AA1=2,D是AB的中点. (I)求AC1与平面B1BCC1所成角的正切值; (II)求证:AC1∥平面B1DC; 试题详情
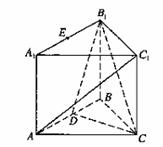
解:(I)∵直三棱柱ABC―A1B1C1,∴B1B⊥面ABC,
试题详情
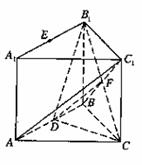
连结BC1,则∠AC1B为AC1与平面B1BCC1所成角.……3分
试题详情
依题设知,BC1=2 ,在Rt△ABC1中, ,在Rt△ABC1中, 试题详情
 …………5分 …………5分 (II)如图,连结DF,在△ABC1中,∵D、F分别为AB、BC1, 的中点, 试题详情
∴DF∥AC1,又∵DF 平面B1DC,AC1 平面B1DC,AC1 平面B1DC, 平面B1DC, ∴AC1∥平面B1DC.………………………………10分 试题详情
(III)PB1=x, 试题详情
当点P从E点出发到A1点,即 时,由(1)同理可证PB1⊥面BB1C1C, 时,由(1)同理可证PB1⊥面BB1C1C, 试题详情
试题详情
当点P从A1点运动到A点,即 时, 时, . . 试题详情
∴三棱锥P―BCC1的体积表达式 试题详情

(I)求证:平面B1AC⊥平面ABB1A1; (II)求直线A1C与平面B1AC所成角的正弦值; (III)求二面角B―B1C―A的大小. 解法一: (I)证明:由直三棱柱性质,B1B⊥平面ABC, ∴B1B⊥AC, 又BA⊥AC,B1B∩BA=B, ∴AC⊥平面 ABB1A1,
试题详情
又AC 平面B1AC, 平面B1AC, ∴平面B1AC⊥平面ABB1A1. …………4分 (II)解:过A1做A1M⊥B1A1,垂足为M,连结CM, ∵平面B1AC⊥平面ABB1A,且平面B1AC∩平面ABB1A1=B1A, ∴A1M⊥平面B1AC. 试题详情
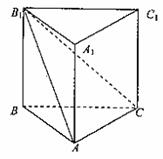
∵直线B1C与平面ABC成30°角, ∴∠B1CB=30°.
试题详情
设AB=BB1=a,可得B1C=2a,BC= , , 试题详情
试题详情
∴直线A1C与平面B1AC所成角的正弦值为 …………9分 …………9分 (III)解:过A做AN⊥BC,垂足为N,过N做NO⊥B1C,垂足为O,连结AO, 由AN⊥BC,可得AN⊥平面BCC1B1,由三垂线定理,可知AO⊥B1C, ∴∠AON为二面角B―B1C―A的平面角, 试题详情
试题详情
∴二面角B―B1C―A的大小为 …………14分 …………14分 试题详情
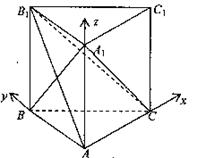
(I)证明:同解法一. …………4分 (II)解:建立如图的空间直角坐标系A―xyz, ∵直线B1C与平面ABC成30°角, ∴∠B1CB=30°. 设AB=B1B=1,
试题详情
试题详情
试题详情
∴直线A1C与平面B1AC所成角的正弦值为 …………9分 …………9分 试题详情
(III)解:设 为平面BCC1B1的一个法向量, 为平面BCC1B1的一个法向量, 试题详情
试题详情
∴二面角B―B1C―A的大小为 试题详情
16、 (北京市东城区2008年高三综合练习二)如图,在四棱锥P―ABCD中,平面PAB⊥平面ABCD,底面ABCD是边长为2的正方形,△PAB为等边三角形. (北京市东城区2008年高三综合练习二)如图,在四棱锥P―ABCD中,平面PAB⊥平面ABCD,底面ABCD是边长为2的正方形,△PAB为等边三角形. (1)求PC与平面ABCD所成角的大小; (2)求二面角B―AC―P的大小; (3)求点A到平面PCD的距离. 试题详情

解法二: 试题详情
 (1)解:同解法一………………5分 (1)解:同解法一………………5分
(2)解:建立如图的空间直角坐标系O―xyz, 则A(-1,0,0),B(1,0,0), 试题详情
则P(0,0, ),C(1,2,0) ),C(1,2,0) 试题详情
设 为平面PAC的一个法向量, 为平面PAC的一个法向量, 试题详情
则 试题详情
又 试题详情
 令z=1,得 令z=1,得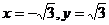 试题详情
得 试题详情
又 是平面ABC的一个法向量, 是平面ABC的一个法向量, 试题详情
设二面角B―AC―P的大小为 , , 试题详情
则 试题详情
 ………………10分 ………………10分
试题详情
(3)解:设 为平面PCD的一个法向量. 为平面PCD的一个法向量. 试题详情
则 由D(-1,2,0),可知 由D(-1,2,0),可知 ), ), 试题详情
 可得a=0,令 可得a=0,令 ,则c=2. ,则c=2. 试题详情
得 , , 试题详情
设点A到平面PCD的距离为d,则 试题详情
∴点A到平面PCD的距离为 试题详情
17、 (北京市丰台区2008年4月高三统一练习一)已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,E、F分别是AC和BC边上的点,且满足 (北京市丰台区2008年4月高三统一练习一)已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,E、F分别是AC和BC边上的点,且满足 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2). ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2). (Ⅰ) 试判断翻折后直线AB与平面DEF的位置关系,并说明理由; (Ⅱ) 求二面角B-AC-D的大小;
图(1) 试题详情
 (Ⅲ) 若异面直线AB与DE所成角的余弦值为 (Ⅲ) 若异面直线AB与DE所成角的余弦值为 ,求k的值. ,求k的值.
解:(Ⅰ) AB∥平面DEF. 在△ABC中, 试题详情
∵ E、F分别是AC、BC上的点,且满足 , , ∴ AB∥EF.
图(2) 试题详情
 ∵ AB ∵ AB 平面DEF,EF 平面DEF,EF 平面DEF,∴ AB∥平面DEF.
…………… 3分 平面DEF,∴ AB∥平面DEF.
…………… 3分
(Ⅱ)过D点作DG⊥AC于G,连结BG, ∵ AD⊥CD, BD⊥CD, ∴ ∠ADB是二面角A-CD-B的平面角. 试题详情
∴ ∠ADB= , 即BD⊥AD. , 即BD⊥AD. ∴ BD⊥平面ADC. ∴ BD⊥AC. ∴ AC⊥平面BGD. ∴ BG⊥AC . ∴ ∠BGD是二面角B-AC-D的平面角. ……………………………… 5分 试题详情
在ADC中,AD=a, DC= , AC=2a, , AC=2a, 试题详情
∴  . . 试题详情
在Rt△BDG中, . . 试题详情
∴  . . 试题详情
即二面角B-AC-D的大小为 .………………………………… 8分 .………………………………… 8分 (Ⅲ)∵ AB∥EF, ∴ ∠DEF(或其补角)是异面直线AB与DE所成的角.… 9分 试题详情
∵  ,∴ ,∴  . . 试题详情
又DC= , ,  , , 试题详情
∴ 试题详情
试题详情
 ………………… 11分 ………………… 11分
试题详情
∴  . . 试题详情
∴  . 解得 k=. . 解得 k=. 试题详情
试题详情
(Ⅰ)求证:平面 ⊥平面 ⊥平面 ; ; 试题详情
(Ⅱ)求证: ∥平面 ∥平面 ; ; 试题详情
(Ⅲ)求二面角 的大小. 的大小. 试题详情
 证明:(Ⅰ)∵PA⊥底面ABCD, 证明:(Ⅰ)∵PA⊥底面ABCD,
试题详情
∴ . . 试题详情
又AB⊥BC, , , 试题详情
∴ ⊥平面 ⊥平面 .
2分 .
2分 试题详情
试题详情
∴平面 ⊥平面 ⊥平面 .
4分 .
4分 (Ⅱ)∵PA⊥底面ABCD, ∴AC为PC在平面ABCD内的射影. 又∵PC⊥AD, ∴AC⊥AD. 试题详情
试题详情
∴ . . 试题详情
又AC⊥AD,故 为等腰直角三角形. 为等腰直角三角形. 试题详情
∴ . . 试题详情
试题详情
在 中, 中, , , 试题详情
∴ 试题详情
又PD 平面EAC,EM 平面EAC,EM 平面EAC, 平面EAC, ∴PD∥平面EAC. 9分 试题详情
试题详情
试题详情
∴ . . 试题详情
试题详情
∴ 就是二面角A―CE―P的平面角.
12分 就是二面角A―CE―P的平面角.
12分 试题详情
试题详情
试题详情
∴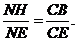 试题详情
代入解得: . . 试题详情
试题详情
即二面角A―CE―P的大小为 . 14分 . 14分 解法二: 试题详情
试题详情
试题详情
设 ,则 ,则 试题详情
 , ,
试题详情
 , ,
试题详情
∴ ,解得: ,解得: . . 试题详情
 . .
试题详情
试题详情
则 .7分 .7分 试题详情
在 中, 中, , , 试题详情
∴ . . 试题详情
又PD 平面EAC,EM 平面EAC,EM 平面EAC, 平面EAC, ∴PD∥平面EAC.
9分 试题详情
试题详情
∴ 试题详情
解得: ,∴ ,∴ .
11分 .
11分 试题详情
试题详情
试题详情
解得: ,∴ ,∴ .
12分 .
12分 试题详情
 .
13分 .
13分
试题详情
∴二面角A―CE―P的大小为 . . 试题详情
试题详情
(Ⅰ)问点 在何处时, 在何处时, ,并加以证明; ,并加以证明; 试题详情
试题详情
(Ⅲ)求二面角 的大小. 的大小. 试题详情
解法一: (Ⅰ)当E为PC中点时, .………2分 .………2分 试题详情
连接AC,且 ,由于四边形ABCD为正方形, ,由于四边形ABCD为正方形, ∴O为AC的中点,又E为中点, ∴OE为△ACP的中位线, 试题详情
试题详情
∴ ………………………5分 ………………………5分 试题详情
试题详情
∴PC⊥DE,PC⊥BE ,又 , , 试题详情
∴ ,PE即为所求, ,PE即为所求,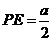 试题详情
试题详情
(Ⅲ)连接PO,则 , , 试题详情
∴ ,又BO⊥AC, ,又BO⊥AC, 试题详情
∴ 试题详情
试题详情
由三垂线定理得 . . 试题详情
 为二面角 为二面角 的平面角. ………………………12分 的平面角. ………………………12分
试题详情
试题详情
试题详情
故 .
……………………………………14分 .
……………………………………14分 解法二: 试题详情
试题详情
试题详情
∴ , , , , 试题详情
试题详情
设面 的法向量为 的法向量为 试题详情
  , ……………… 7分 , ……………… 7分
试题详情
试题详情
试题详情
试题详情
 . . 
试题详情
试题详情
试题详情
(Ⅰ)求证: ; ;
试题详情
(Ⅱ)求二面角 的大小; 的大小; 试题详情
(Ⅲ)求异面直线 和 和 所成角的大小. 所成角的大小. 解法一: (Ⅰ)证明: 试题详情
试题详情
且 , ,
 . …………..
2分 . …………..
2分 试题详情
试题详情
又 试题详情
  .
………….. 4分 .
………….. 4分
(Ⅱ)解: 试题详情
试题详情
试题详情
根据三垂线定理得  , , 试题详情
 是二面角 是二面角 的平面角.
………….. 6分 的平面角.
………….. 6分
试题详情
试题详情
 , ,  , ,
试题详情
 ,
…………..
8分 ,
…………..
8分
试题详情
即二面角 的大小是 的大小是 .
………….. 9分 .
………….. 9分 (Ⅲ)解: 试题详情
试题详情
 连结 连结 . .
试题详情
试题详情
 , ,
试题详情
 , ,  , ,
试题详情
 . .
试题详情
试题详情
在 中, 中, ,
………….. 13分 ,
………….. 13分 试题详情
试题详情
试题详情
试题详情
 平面 平面 . .
试题详情
试题详情
试题详情
 轴, 轴, 轴,建立空间直角坐标系 . ………….. 2分 轴,建立空间直角坐标系 . ………….. 2分
试题详情
 . . 
试题详情
 . .
试题详情
 , ,
试题详情
 . .
试题详情
试题详情
试题详情

 . .
试题详情
又 试题详情
  .
………….. 7分 .
………….. 7分
(Ⅱ)解: 试题详情
试题详情
试题详情
 是二面角 是二面角 的平面角.
………….. 8分 的平面角.
………….. 8分
试题详情
在 中, 中,  , , 试题详情
 从而 从而 , ,
试题详情
 ,
………….. 10分 ,
………….. 10分
试题详情
即二面角 的大小是 的大小是 .
………….. 11分 .
………….. 11分 (Ⅲ)解: 试题详情
 , ,
试题详情
 , ,
试题详情
试题详情
21、(北京市西城区2008年5月高三抽样测试)如图,在正四棱柱ABCD―A1B1C1D1中,AA1= ,AB=1,E是DD1的中点。 ,AB=1,E是DD1的中点。 试题详情
 (Ⅰ)求直线B1D和平面A1ADD1所成角的大小; (Ⅰ)求直线B1D和平面A1ADD1所成角的大小;
(Ⅱ)求证:B1D⊥AE; (Ⅲ)求二面角C―AE―D的大小。 试题详情
试题详情
试题详情
试题详情
22、(北京市宣武区2008年高三综合练习一)如图,三棱锥P-ABC中,PC 平面ABC,PC=AC=2, 平面ABC,PC=AC=2, 试题详情
AB=BC,D是PB上一点,且CD 平面PAB 平面PAB 试题详情
 (1)求证:AB (1)求证:AB 平面PCB; 平面PCB;
(2)求异面直线AP与BC所成角的大小; (3)求二面角C-PA-B 的大小的余弦值。 试题详情
试题详情
 PC PC AB, AB,
试题详情
试题详情
试题详情
 AB AB  平面PCB 平面PCB
(2)过点A作AF//BC,且AF=BC,连结PF、FC, 试题详情
则 为异面直线PA与BC所成的角。 为异面直线PA与BC所成的角。 试题详情
试题详情
有三垂线定理,得PF  AF,则AF=CF= AF,则AF=CF= , , 试题详情
PF= 。 。 试题详情
在Rt 中, 中, , , 试题详情
 异面直线PA与BC所成的角为 异面直线PA与BC所成的角为 ………………………………………… 8分 ………………………………………… 8分
(3)取AP的中点E,连结CE、DE 试题详情
试题详情
试题详情
  为二面角C-PA-B的平面角 为二面角C-PA-B的平面角
试题详情
试题详情
试题详情
在Rt 中, 中,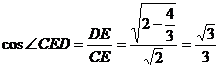 试题详情
 二面角C-PA-B大小的余弦值为 二面角C-PA-B大小的余弦值为 ……………………………………..13分 ……………………………………..13分
解法二:(1)同解法一
………………………………………………………4分 试题详情
(2)由(1)AB  平面PCB , 平面PCB , PC=AC=2, PC=AC=2, 试题详情
又 AB=BC, 可求得BC= AB=BC, 可求得BC=  以B为原点,如图建立空间直角坐标系, 试题详情
则A(0, ,0),B(0,0,0), C( ,0),B(0,0,0), C( ,0,0) ,0,0) 试题详情
P( ,0,2) ,0,2) 试题详情
试题详情
试题详情
试题详情
 异面直线AP与BC所成的角为 异面直线AP与BC所成的角为 ………………………………………………8分 ………………………………………………8分
(3)设平面PAB的法向量为m=(x,y,z) 试题详情
试题详情
则 ,即,得m=( ,即,得m=( ,0,-1) ,0,-1) 设平面PAC的法向量为n=(x,y,z) 试题详情
试题详情
Cos<m,n>= 试题详情
 二面角C-PA-B大小的余弦值为 二面角C-PA-B大小的余弦值为
试题详情
23、 (北京市宣武区2008年高三综合练习二)如图所示,正三棱柱 (北京市宣武区2008年高三综合练习二)如图所示,正三棱柱 的底面边长是2,侧棱长是,D是AC的中点。 的底面边长是2,侧棱长是,D是AC的中点。 试题详情
(1)求证: 平面 平面 ; ; 试题详情
(2)求二面角 的大小; 的大小; 试题详情
(3)求直线 与平面 与平面 所成的角的正弦值。 所成的角的正弦值。 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
又 BD BD AC AC 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
(3)由(2)作AM  ,M为垂足。 ,M为垂足。 试题详情
试题详情
试题详情
试题详情
 BD BD AM AM
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
 直线 直线 与平面 与平面 D所成的角的正弦值为 D所成的角的正弦值为
解法二: (1)同解法一 (2)如图建立空间直角坐标系, 试题详情
试题详情
试题详情
设平面 的法向量为n=(x,y,z) 的法向量为n=(x,y,z) 试题详情
则n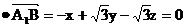 试题详情
n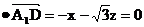 试题详情
则有 ,得n=( ,得n=( ,0,1) ,0,1) 试题详情
由题意,知 =(0,0, =(0,0, )是平面ABD的一个法向量。 )是平面ABD的一个法向量。 试题详情
设n与 所成角为 所成角为 , , 试题详情
则 , , 试题详情
试题详情
试题详情
试题详情
则 试题详情
试题详情
24、(四川省成都市高2008届毕业班摸底测试)如图,在直三棱柱ABC―A1B1C1中,已知AB=BC=1,∠ABC=90°,AA1= ,D、E分别为BB1、AC的中点。 ,D、E分别为BB1、AC的中点。 试题详情
 (Ⅰ)求二面角A1―AD―C1的大小; (Ⅰ)求二面角A1―AD―C1的大小;
试题详情
(Ⅱ)若 ,求证:BE//平面AC1D。 ,求证:BE//平面AC1D。 试题详情
(Ⅰ)以BA所在的直线为x轴、BC所在直线为y轴、BB1所在直线为z轴,建立空间直角坐标系 。∵ 。∵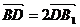 则A(1,0,0),A1(1,0,3),C1(0,1,3), D(0,0,2) 试题详情
∴ ……2分 ……2分 设平面AC1D的法向量为n=(x,y,z),则由 试题详情
试题详情
 ∴平面AC1D的法向量为n=(2,-1,1) …………2分 ∴平面AC1D的法向量为n=(2,-1,1) …………2分
又平面A1AD的法向量为m=(0,1,0) …………1分 试题详情
∵ , , 又由图形可知,所求二面角为锐角 试题详情
∴二面角A1―AD―C1的大小为arccos . …………2分 . …………2分 (Ⅱ)作EF//CC1交AC1于点F,连结DF。 试题详情
∵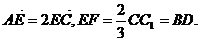 又EF//BD, ∴四边形EFDB为平行四边形,∴DF//BE。 试题详情
而DF 平面AC1D,BE 平面AC1D,BE 平面AC1D, 平面AC1D, ∴BE//平面AC1D。 …………5分) 试题详情
[注:也可证 ] ] 试题详情
25、(东北区三省四市2008年第一次联合考试)如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点, 试题详情
 且CD⊥平面PAB。 且CD⊥平面PAB。
(1)求证:AB⊥平面PCB (2)求二面角C-PA-B的大小。 试题详情
解(1) 试题详情
 
(2)解法一: 取AP的中点E,连续CE、DE 试题详情
试题详情
试题详情
试题详情

(2)解法二: 试题详情
试题详情
试题详情
试题详情
试题详情
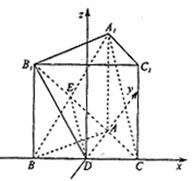
26、(东北三校2008年高三第一次联考) 如图,正三棱柱 如图,正三棱柱 的所有棱长都为4,D为CC1中点. 的所有棱长都为4,D为CC1中点. 试题详情
(Ⅰ)求证: ; ; 试题详情
(Ⅱ)求二面角 的大小. 的大小. 解法一:(Ⅰ)取BC中点O,连结AO. 试题详情
试题详情
试题详情
 的中点, 的中点,
试题详情
由正方形性质知 , , 试题详情
 .………5分 .………5分
试题详情
又在正方形 中, 中, , , 试题详情
 平面 平面 .……6分 .……6分
试题详情
(Ⅱ)设AB1与A1B交于点 ,在平面 ,在平面 1BD中, 1BD中, 试题详情
试题详情
 为二面角 为二面角 的平面角.………9分 的平面角.………9分
试题详情
在 中,由等面积法可求得 中,由等面积法可求得 ,………10分 ,………10分 试题详情
又 , , . . 试题详情
所以二面角 的大小为 的大小为 .……12分 .……12分 试题详情
试题详情
试题详情
如图建立空间直角坐标系 , , 试题详情
则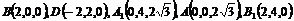 试题详情
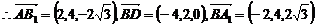
……3分 试题详情
试题详情
 平面 平面 .………6分 .………6分
试题详情
试题详情
试题详情
试题详情
试题详情
由(Ⅰ) 为平面 为平面 的法向量.……10分 的法向量.……10分 试题详情
试题详情
试题详情
 (1)求证: (1)求证: ; ;
试题详情
试题详情
试题详情
解:(1)由于
 , , ,根据三垂线定理, ,根据三垂线定理, 试题详情
得 .
(4分) .
(4分) 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
28、 (本小题满分12分) 如图,正三棱柱ABC―A1B1C1中,D是BC的中点,AA1=AB=1. (本小题满分12分) 如图,正三棱柱ABC―A1B1C1中,D是BC的中点,AA1=AB=1.
(I)求证:A1C//平面AB1D;
(II)求二面角B―AB1―D的大小;
(III)求点C到平面AB1D的距离.
【解】解法一(I)证明: 连接A1B,设A1B∩AB1 = E,连接DE. ∵ABC―A1B1C1是正三棱柱,且AA1 = AB, ∴四边形A1ABB1是正方形, ∴E是A1B的中点, 又D是BC的中点, ∴DE∥A1C.
………………………… 3分 试题详情
∵DE 平面AB1D,A1C 平面AB1D,A1C 平面AB1D, 平面AB1D, ∴A1C∥平面AB1D. ……………………4分 (II)解:在面ABC内作DF⊥AB于点F,在面A1ABB1内作FG⊥AB1于点G,连接DG. ∵平面A1ABB1⊥平面ABC, ∴DF⊥平面A1ABB1, ∴FG是DG在平面A1ABB1上的射影, ∵FG⊥AB1, ∴DG⊥AB1 ∴∠FGD是二面角B―AB1―D的平面角 …………………………6分 试题详情
设A1A = AB = 1,在正△ABC中,DF= 试题详情
在△ABE中, ,在Rt△DFG中, ,在Rt△DFG中, , , 试题详情
所以,二面角B―AB1―D的大小为 …………………………8分 …………………………8分 (III)解:∵平面B1BCC1⊥平面ABC,且AD⊥BC, 试题详情
∴AD⊥平面B1BCC1,又AD 平面AB1D,∴平面B1BCC1⊥平面AB1D. 平面AB1D,∴平面B1BCC1⊥平面AB1D. 在平面B1BCC1内作CH⊥B1D交B1D的延长线于点H, 则CH的长度就是点C到平面AB1D的距离. ……………………………10分 试题详情
由△CDH∽△B1DB,得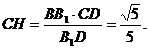 试题详情
解法二: 建立空间直角坐标系D―xyz,如图, (I)证明: 连接A1B,设A1B∩AB1 = E,连接DE. 设A1A = AB = 1,
试题详情
则 试题详情
试题详情
 …………………………3分 …………………………3分
试题详情
 , ,
试题详情
 ……………………………………4分 ……………………………………4分
试题详情
(II)解: , ,  , , 试题详情
设 是平面AB1D的法向量,则 是平面AB1D的法向量,则 , , 试题详情
故 ; ; 试题详情
同理,可求得平面AB1B的法向量是 ……………………6分 ……………………6分 试题详情
设二面角B―AB1―D的大小为θ, , , 试题详情
∴二面角B―AB1―D的大小为 …………………………8分 …………………………8分 试题详情
(III)解由(II)得平面AB1D的法向量为 , , 试题详情
取其单位法向量 试题详情
∴点C到平面AB1D的距离 试题详情
29、(福建省莆田一中2007~2008学年上学期期末考试卷)如图所示,等腰△ABC 的底边AB=6 ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将 ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将 △BEF折起到△PEF的位置,使PE⊥AE.记 △BEF折起到△PEF的位置,使PE⊥AE.记 V(x)表示四棱锥P-ACFE的体积. V(x)表示四棱锥P-ACFE的体积. (1)求V(x)的表达式; (2)当x为何值时,V(x)取得最大值? (3)当V(x)取得最大值时,求异面直线AC与PF所成角的余弦值。 试题详情
试题详情
试题详情
试题详情
试题详情
 ,设异面直线AC与PF夹角是 ,设异面直线AC与PF夹角是 试题详情
试题详情
30、(福建省泉州一中高2008届第一次模拟检测)如图,平面PAD⊥平面ABCD, ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E、F、G 分别是线段PA、PD、CD的中点.
1,3,5 (2)求异面直线EG与BD所成的角; (3)在线段CD上是否存在一点Q,使得A点到平面
试题详情
EFQ的距离为0.8,若存在,求出CQ的值; 若不存在,请说明理由. 试题详情

∴PB∥平面EFG. (2)解:取BC的中点M,连结GM、AM、EM,则GM//BD, 试题详情

所成的角.
试题详情
在Rt△MAE中,  , , 试题详情
同理 , , 试题详情
又GM= , , ∴在△MGE中, 试题详情
试题详情
故异面直线EG与BD所成的角为arccos , , (3)假设在线段CD上存在一点Q满足题设条件, 试题详情

∵ABCD是正方形,△PAD是直角三角形,且PA=AD=2, ∴AD⊥AB,AD⊥PA. 又AB∩PA=A, ∴AD⊥平面PAB. 又∵E,F分别是PA,PD中点, ∴EF∥AD,∴EF⊥平面PAB.
试题详情
又EF 面EFQ, 面EFQ, ∴面EFQ⊥面PAB. 过A作AT⊥ER于T,则AT⊥平面EFQ, ∴AT就是点A到平面EFQ的距离. 试题详情
设 , , 试题详情
在 , , 试题详情
解得 试题详情
故存在点Q,当CQ= 时,点A到平面EFQ的距离为0.8. 时,点A到平面EFQ的距离为0.8. 解法二:建立如图所示的空间直角坐标系A-xyz, 则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0), 试题详情
| | | | | | | | | | | | | | | | | | | | | | | | | | | |

 1、(广东省广州执信中学、中山纪念中学、深圳外国语学校三校期末联考)(本小题满分12分)如图,直四棱柱ABCD―A1B
1、(广东省广州执信中学、中山纪念中学、深圳外国语学校三校期末联考)(本小题满分12分)如图,直四棱柱ABCD―A1B