
A.①②④ B.②③④ C.②④⑤ D.②③⑤
试题详情
10. 广东省梅州揭阳两市四校2008届高三第三次联考数学理科试卷 试题详情
设 ,则对任意实数 ,则对任意实数 , , 是 是 的 的 A. 充分必要条件 B.
充分而不必要条件 C. 必要而不充分条件
D. 既不充分也不必要条件 试题详情
试题详情
试题详情
11. 广东省梅州揭阳两市四校2008届高三第三次联考数学文科试题 试题详情
试题详情
试题详情
试题详情
试题详情
已知函数 ,则 ,则 试题详情
A. B. B.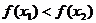 试题详情
C. D. D. 的大小不能确定 的大小不能确定 试题详情
试题详情
试题详情
A. B. B.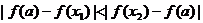 试题详情
C. D. D.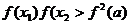 试题详情
试题详情
A. B.
B.
试题详情
试题详情
C 特值法:令a=2与可知 在 在 上恒正,显然选项 上恒正,显然选项
D不正确 试题详情
15. 已知f(x+y)=f(x)?f(y)对任意的实数x、y都成立,且f(1)=2,则+++…++= _________. 4012 [解析]∵f(1+0)=f(1)?f(0),2=2f(0),∴f(0)=1
∵f(2)=f(1+1)=f(1)?f(1)=22,
f(3)=f(2+1)=f(2)?f(1)=23,
依此类推:f(2005)=22005,f(2006)=22006, 试题详情
∴原式= =4012. =4012. 试题详情
16. 已知函数 的图象如右图示,函数 的图象如右图示,函数 的图象与 的图象与 试题详情
试题详情
A. B. B.
 试题详情
试题详情
试题详情
试题详情
试题详情
A.  B. B.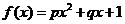 试题详情
试题详情
试题详情
18. 若函数 的一个正数零点附近的函数值用二分法计算,其参考数据如下: 的一个正数零点附近的函数值用二分法计算,其参考数据如下: f (1) = -2 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
那么方程 的一个近似根(精确到0.1)为( )。 的一个近似根(精确到0.1)为( )。 试题详情
试题详情
C
解:f(1.40625)=-0.054< 0,f(1.4375)=0.162> 0 且都接近0,由二分法可知其根近似于1.4。 试题详情
试题详情
当x<0时,2x<1, f(x) =2x; x>0时,2x>1,
f(x) =1. 答案:A 试题详情
20. 已知定义域为(-1,1)的奇函数y=f (x)又是减函数,且f (a-3)+f
(9-a2)<0,则a的取值范围是 试题详情
试题详情
试题详情
试题详情
解析: ,答案:C ,答案:C 试题详情
试题详情
试题详情
试题详情
则平面区域 所围成的面积是 所围成的面积是 A.2 B.4
C.5 D.8 试题详情
试题详情
试题详情
试题详情
A. B. B.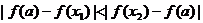 试题详情
C. D. D.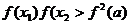 试题详情
26. 如图所示,已知D是面积为1的△ABC的边AB上任一点,E是边AC上 试题详情
试题详情
且 ,记△BDF的面积为S=f( ,记△BDF的面积为S=f( ),则S的最大值是( D
) ),则S的最大值是( D
) 试题详情
试题详情
27. 函数 的零点所在的大致区间是 的零点所在的大致区间是 试题详情
试题详情
试题详情
试题详情
A
根据反函数的性质,即求当x > 1时,函数 的值域,此后注意到 的值域,此后注意到 在 在 上递增即可获解. 上递增即可获解. 【命题动向】本题考查反函数的概念与性质,函数的单调性,函数值域的求法,灵活驾驶基础知识和基本方法的能力. 试题详情
29. 已知函数 的值为 的值为 A.-4 B.2 C.0 D.-2 试题详情
30. 计算机的价格大约每3年下降 ,那么今年花8100元买的一台计算机,9年后的价格大约是 ,那么今年花8100元买的一台计算机,9年后的价格大约是 A. 2400元 B. 900元 C. 300元 D. 100元 试题详情
9年后的价格大约是 元,选C. 元,选C. 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
31. 在某种新型材料的研制中,实验人员获得了右边一组实验数据:现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是 试题详情
试题详情
由该表提供的信息知,该模拟函数在 应为增函数,故排除D,将 应为增函数,故排除D,将 、4…代入选项A、B、C易得B最接近,故答案应选B. 、4…代入选项A、B、C易得B最接近,故答案应选B. 试题详情
试题详情
⑴ ⑵
⑵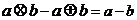 试题详情
⑶ ⑷
⑷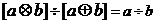 A. ⑴、⑵、⑶、⑷ B. ⑴、⑵、⑶ C. ⑴、⑶
D.⑵、⑷ 由定义知⑴、⑶恒成立,⑵⑷不恒成立,正确答案C. 试题详情
33. 若函数 的最大值为 的最大值为 A.3 B.6 C.9 D.10 试题详情
试题详情
35. 设[x]表示不超过x的最大整数,则满足不等式[x]2-3[x]-10≤0的解集是
( ) A.[-1,5) B.[-1,6)
C.(-3,6) D.[-2,6) 由[x]2-3[x]-10≤0得-2≤[x] ≤5,则-2≤x≤6,故选D. 试题详情
试题详情
试题详情
37.已知 ,且已知集合 ,且已知集合 ,则集合 ,则集合 的元素个数有( ) 的元素个数有( ) A.2个 B.3个 C.4个 D.无数个 . 试题详情
试题详情
试题详情
试题详情
运动时,在映射 的作用下,动点 的作用下,动点 的轨迹是 的轨迹是 试题详情
试题详情
39. 若函数 ,则 ,则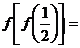 试题详情
(A)  (B) 0
(C) (B) 0
(C)  (D)
1 (D)
1 试题详情
试题详情
试题详情
 且 且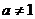 试题详情
42. 设函数f (x)=ax2+bx-c (a≠0)对任意实数t都有f (2+t)=f (2-t)成立,
在函数值f (-1),f (1),f (2),f (5)中最小的一个不可能是
( ) A.f (-1) B.f (1) C.f (2)
D.f(5) 试题详情
43. 定义一种运算“*”:对于自然数n满足以下运算性质: (i)1*1=1,(ii)(n+1)*1=n*1+1,则n*1等于 试题详情
A.n
B.n+1
C.n -1
D. 试题详情
44. 已知两个函数 和 和 的定义域和值域都是集合{1,2,3},其定义如下表. 的定义域和值域都是集合{1,2,3},其定义如下表. x 1 2 3 f(x) 2 3 1 x 1 2 3 g(x) 1 3 2 试题详情
填写下列 的表格,其三个数依次为 的表格,其三个数依次为 x 1 2 3 g
(f(x)) A. 3,1,2 B
. 2,1,3 C. 1,2,3 D. 3,2,1 试题详情
45. 在实数的原有运算法则中,我们补充定义新运算“ ”如下: ”如下: 试题详情
当 时, 时, ; ; 试题详情
当 时, 时, 。 。 试题详情
则函数 的最大值等于( C
) 的最大值等于( C
) (“?”和“-”仍为通常的乘法和减法) 试题详情
A.  B.
1 C. 6 D.
12 B.
1 C. 6 D.
12 试题详情
46、已知定义域为R的函数 为增函数,且函数 为增函数,且函数 为偶函数,则下列结论不成立的是 为偶函数,则下列结论不成立的是 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
A.5 B. C.13
D. C.13
D.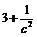 试题详情
50. 若一系列函数的解析式相同,值域相同但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为 ,值域为{3,19}的“孪生函数”共有 ,值域为{3,19}的“孪生函数”共有 A.15个 B.12个 C.9个 D.8个 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
54. 已知函数 ,则 ,则 的值为( ) 的值为( ) 试题详情
试题详情
55.
若 ,则函数 ,则函数 与 与 的图像关于 的图像关于 A.x轴对称 B.y轴对称 C.直线y=x对称 D.原点对称 试题详情
试题详情
试题详情
57. 上海市浦东新区2007学年度第一学期期末质量抽测2008/1 试题详情
三、解答题: 1、  某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图). 某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图). (1)分别写出两种产品的收益与投资的函数 关系; (2)该家庭现有20万元资金,全部用于理 财投资,问:怎样分配资金能使投资获 得最大收益,其最大收益为多少万元? [解]: 试题详情
试题详情
试题详情
(2)设:投资债券类产品 万元,则股票类投资为 万元,则股票类投资为 万元 万元 试题详情
  -------------------8分 -------------------8分
试题详情
试题详情
所以当 ,即 ,即 万元时,收益最大, 万元时,收益最大, 万元.----------------14分 万元.----------------14分 上海市静安区2007学年第一学期高三期末质量监控考试数学试题 试题详情
2、设 ( ( 为实常数). 为实常数). 试题详情
(1)
当 时,证明: 时,证明: 不是奇函数; 不是奇函数; 试题详情
试题详情
试题详情
(文)求(2)中函数 的值域. 的值域. 试题详情
试题详情
试题详情
化简整理得 ,这是关于 ,这是关于 的恒等式,所以 的恒等式,所以 试题详情
试题详情
试题详情
而 对任何实数 对任何实数 成立; 成立;
试题详情
所以对任何实数 、c都有 、c都有 成立. 成立.
试题详情
(文)  ,因为 ,因为 , ,
试题详情
所以 , , , ,
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
所以在函数f(x)的定义域R上,值域为[-M,-m] [m,M](※).(2分) [m,M](※).(2分) 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
②若M<0,由 ,m<0得:M>m,进一步m<M<-M<-m,由(※)得:在函数f(x)的定义域上,值域改写为[m,M] ,m<0得:M>m,进一步m<M<-M<-m,由(※)得:在函数f(x)的定义域上,值域改写为[m,M] [-M,-m], [-M,-m], 试题详情
所以 .(4分) .(4分) 试题详情
试题详情
试题详情
试题详情
(1)只需要证明 , , 试题详情
即要证明 在 在 上单调减. (2分) 上单调减. (2分) 试题详情
因为 ,(2分), ,(2分), 试题详情
试题详情
试题详情
试题详情
经过计算得: =-3,(2分), =-3,(2分), 试题详情
 ,(2分), ,(2分),
试题详情
所以 ,解得: ,解得: . (2分). . (2分). 试题详情
5. 上海市杨浦区2007学年度第一学期高三学科测试数学试卷 试题详情
已知向量 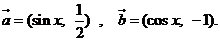 试题详情
(1)当 时, 求 时, 求 的值. 的值. 试题详情
(2)(文科考生做)
求 ? ? 的最大值与最小值. 的最大值与最小值. 试题详情
(理科考生做)求 ? ? , 在 , 在 上的最大值与最小值. 上的最大值与最小值. [解] (1)(文) 试题详情
试题详情
(理)A={x|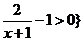 试题详情
 ∴ -1<x<1 ∴ -1<x<1 ∴A=(-1,1),定义域关于原点对称 试题详情
f(x)= lg , , 试题详情
试题详情
(2)B={x|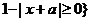 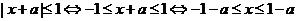 B=[-1-a,1-a] 当a ³2时, -1-a£-3, 1-a£-1, 试题详情
由A=(-1,1), B=[-1-a,1-a], 有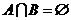 试题详情
反之,若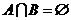 ,可取-a-1=2,则a=-3,a小于2. (注:反例不唯一) ,可取-a-1=2,则a=-3,a小于2. (注:反例不唯一) 试题详情
所以,a ³2是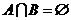 的充分非必要条件。 的充分非必要条件。 试题详情
试题详情
试题详情
试题详情
(理) ,即 ,即 ,故x<0或x>1. ,故x<0或x>1. 试题详情
∴  或 或 . . 试题详情
试题详情
试题详情
解得x<0或x>1或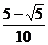  . . 试题详情
试题详情
(文)由已知 , , . . 试题详情
∴  在(-∞, 在(-∞, 上单增,在(2,+∞)上单调. 上单增,在(2,+∞)上单调. 试题详情
又∵  , , . . 试题详情
∴ 需讨论 与 与 的大小. 的大小. 试题详情
由 知 知 试题详情
试题详情
故 时,应有 时,应有 . . 试题详情
试题详情
已知函数 ,在区间 ,在区间 上有最大值5,最小值2。 上有最大值5,最小值2。 (1)求a,b的值。 试题详情
(2)若 上单调,求m的取值范围。 上单调,求m的取值范围。 试题详情
解(1) (1分) (1分) 试题详情
①当 时, 时, 上为增函数 上为增函数 试题详情
故 (3分)
(3分) 试题详情
②当 上为减函数 上为减函数 试题详情
故 (3分) (3分) 试题详情
(2)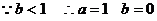 试题详情
即 (1分) (1分) 试题详情
 (1分) (1分) 试题详情
试题详情
即 (1分) (1分) 试题详情
8. 江苏省省阜中2008届高三第三次调研考试数学(文科)试题 试题详情
已知函数 , , . . 试题详情
(1)当 时,若 时,若 上单调递减,求a的取值范围; 上单调递减,求a的取值范围; 试题详情
试题详情
试题详情
(1)当 时, 时, , , 试题详情
试题详情
试题详情
试题详情
试题详情
故 ,∴ ,∴ 为二次函数, 为二次函数,
试题详情
试题详情
此时, 时, 时, 有最大值. 有最大值. 试题详情
又 取最小值时, 取最小值时, , ,
试题详情
依题意,有 ,则 ,则 , , 试题详情
试题详情
∴满足条件的整数对 是 是 . (6分) . (6分) 试题详情
(3)当整数对是 时, 时,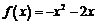 试题详情
 , , 是以2为周期的周期函数, 是以2为周期的周期函数,
试题详情
试题详情
 , ,
试题详情
故 (6分) (6分) 试题详情
9. 江苏省泗洪县实验中学2007-2008学年高三第三次月考 试题详情
函数f(x)的定义域为D  , 满足: 对于任意 , 满足: 对于任意 ,都有 ,都有 试题详情
 ,且f(2)=1. ,且f(2)=1.
(1)求f(4)的值; 试题详情
(2)如果 上是单调增函数,求x的取值范围. 上是单调增函数,求x的取值范围. 试题详情
(1) ………………………5分
………………………5分 试题详情
(2) 3=2+1= ………………………9分
………………………9分 试题详情
因为 上是增函数,所以 上是增函数,所以 试题详情
 ……………………13分
……………………13分
试题详情
即x的取值范围是 ………………………14分
………………………14分 试题详情
试题详情
王小明同学采用先建立直角坐标系,再求关系式的方法,他写道: 试题详情
试题详情
解: 5分 5分 试题详情
试题详情
试题详情
即有 11分 11分 试题详情
试题详情
解得 , , 14分 14分 试题详情
所以符合要求的函数是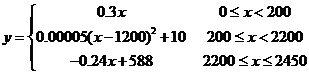 试题详情
试题详情
已知函数 是偶函数。 是偶函数。
(I)求k的值; 试题详情
(II)若方程 的取值范围。 的取值范围。 试题详情
解:(I)由函数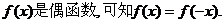 试题详情
 …………2分 …………2分
试题详情
试题详情
 …………4分 …………4分
试题详情
 …………6分 …………6分
试题详情
(II)由 , , 试题详情
 …………8分 …………8分
试题详情
 , …………10分 , …………10分
试题详情
试题详情
故要使方程 …………12分 …………12分 试题详情
12. 江苏省如皋中学2007―2008学年度第二学期阶段考试高三数学(理科) 试题详情
试题详情
(Ⅰ)判断函数 在定义域内的单调性,并证明。 在定义域内的单调性,并证明。 试题详情
试题详情
证一:设 试题详情
试题详情
则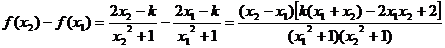 试题详情
又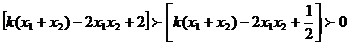 试题详情
试题详情
故 在区间 在区间 上是增函数。 上是增函数。 试题详情
证二: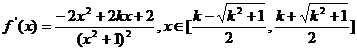 试题详情
易知:当 试题详情
故 在区间 在区间 上是增函数。 上是增函数。 试题详情
二解: 恒成立。4 恒成立。4 试题详情
试题详情
13. 江苏省滨海县08届高三第三次联考数学试卷2008-1-4 据调查,某地区100万从事传统农业的农民,人均收入3000元,为了增加农民的收入,当地政府积极引进资本,建立各种加工企业,对当地的农产品进行深加工,同时吸收当地部分农民进入加工企业工作,据估计,如果有x(x>0)万人进企业工作,那么剩下从事传统农业的农民的人均收入有望提高2x%,而进入企业工作的农民的人均收入为3000a元(a>0)。 (1)在建立加工企业后,要使从事传统农业的农民的年总收入不低于加工企业建立前的农民的年总收入,试求x的取值范围; (2)在(I)的条件下,当地政府应该如何引导农民(即x多大时),能使这100万农民的人均年收入达到最大。 解:(I)由题意得(100-x)?3000?(1+2x%)≥100×3000, 即x2-50x≤0,解得0≤x≤50,
又∵x>0 ∴0<x≤50;
(II)设这100万农民的人均年收入为y元, 则y= = =-[x-25(a+1)]2+3000+475(a+1)2 (0<x≤50) (i)当0<25(a+1)≤50,即0<a≤1,当x=25(a+1)时,y最大; (ii)当25(a+1)>50,即a >1,函数y在(0,50]单调递增,∴当x=50时,y取最大值。 答:在0<a≤1时,安排25(a +1)万人进入企业工作,在a>1时安排50万人进入企业工作,才能使这100万人的人均年收入最大 试题详情
14. 北京奥运会纪念章某特许专营店销售纪念章,每枚进价为5元,同时每销售一枚这种纪念章还需向北京奥组委交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚,经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为x元(x∈N*). (Ⅰ)写出该特许专营店一年内销售这种纪念章所获得的利润y(元)与每枚纪念章的销售价格x的函数关系式(并写出这个函数的定义域); (Ⅱ)当每枚纪念销售价格x为多少元时,该特许专营店一年内利润y(元)最大,并求出这个最大值. 试题详情
(Ⅰ)依题意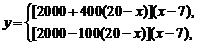 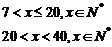 试题详情
∴ 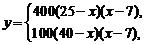 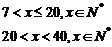 试题详情
此函数的定义域为
试题详情
(Ⅱ)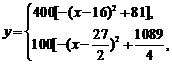 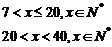 试题详情
试题详情
当 ,因为x∈N*,所以当x=23或24时, ,因为x∈N*,所以当x=23或24时, (元); (元); 试题详情
综合上可得当 时,该特许专营店获得的利润最大为32400元. 时,该特许专营店获得的利润最大为32400元. 试题详情
15. 已知函数 的定义域为 的定义域为 ,且同时满足: ,且同时满足: 试题详情
(1)对任意 ,总有 ,总有 ; ; 试题详情
(2)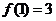 试题详情
试题详情
(I)求 的值; 的值; 试题详情
(II)求 的最大值; 的最大值; 试题详情
试题详情
求证: . . 试题详情
解:(I)令 ,由(3),则 ,由(3),则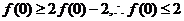 试题详情
由对任意 ,总有 ,总有 (2分)
(2分) 试题详情
试题详情
试题详情
 (6分)
(6分)
试题详情
(III)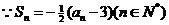 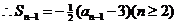 试题详情
 (8分)
(8分)
试题详情
试题详情
 ,即 ,即 。 。
试题详情
 故
故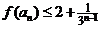
试题详情
 即原式成立。
(14分) 即原式成立。
(14分)
试题详情
试题详情
(1)(文科考生做)当 时,求集合 时,求集合 . . 试题详情
(理科考生做)判定函数 的奇偶性,并说明理由. 的奇偶性,并说明理由. 试题详情
(2)问: 是 是 的什么条件(充分非必要条件 、必要非充分条件、充要条件、既非充分也非必要条件)?并证明你的结论. 的什么条件(充分非必要条件 、必要非充分条件、充要条件、既非充分也非必要条件)?并证明你的结论. [解] (1)(文) 试题详情

∴B[-2,0]
……………………6分 试题详情
(理)A={x|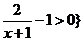 试题详情
 ∴ -1<x<1 ∴ -1<x<1 ∴A=(-1,1),定义域关于原点对称 ……………………3分 试题详情
f(x)= lg , , 试题详情
试题详情
(2)B={x|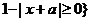 试题详情
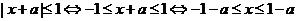
B=[-1-a,1-a]
……………………8分 当a ³2时, -1-a£-3, 1-a£-1, 试题详情
由A=(-1,1), B=[-1-a,1-a], 有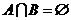 ……………11分
……………11分 试题详情
反之,若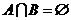 ,可取-a-1=2,则a=-3,a小于2. (注:反例不唯一) ,可取-a-1=2,则a=-3,a小于2. (注:反例不唯一)
……………………13分 试题详情
所以,a ³2是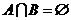 的充分非必要条件. …………………14分 的充分非必要条件. …………………14分 试题详情
17. 我们知道:函数y=f (x)如果存在反函数y=f -1 (x),则y=f (x)的图像与y=f -1 (x)图像关于直线y=x对称。若y=f (x)的图像与y=f -1 (x)的图像有公共点,其公共点却不一定都在直线y=x上;例如函数f (x)= 。 。 (1)若函数y=f (x)在其定义域上是增函数,且y=f (x)的图像与其反函数y=f -1 (x)的图像有公共点,证明这些公共点都在直线y=x上; (2)对问题:“函数f (x)=a x (a>1)与其反函数f -1 (x)=logax的图像有多少个公共点?”有如下观点: 观点①:“当a>1时两函数图像没有公共点,只有当0<a<1时两函数图像才有公共点”。 观点②:“利用(1)中的结论,可先讨论函数f (x)=a x (a>1)的图像与直线y=x的公共点的个数,为此可构造函数F (x)=a x-x(a>1),然后可利用F (x)的最小值进行讨论”。 请参考上述观点,讨论函数f (x)=ax (a>1)与其反函数f -1 (x)=logax图像公共点的个数。 解; 1)设点M(x0, y0)是函数y = f (x)的图像与其反函数y = f -1 (x)的图像的公 点,则有:y0=f (x0) ,
y0 = f -1 (x0),据反函数的意义有:x0 = f (y0)。
………2分 所以:y0 = f (x0)且同时有x0 = f (y0)。 若x0 < y0 ,因为函数y = f (x)
是其定义域上是增函数, 所以有:f (x0) < f (y0) ,即y0 < x0 与
x0 < y0矛盾,这说明x0 < y0是错误的。 同理可证x0 > y0也是错误的。 所以x0 = y0 ,即函数y = f (x)的图像与其反函数y = f -1 (x)的图像有公共点在直线y = x上;
…5分 2)构造函数F (x)=a x-x(a>1) 因为F′ (x)= a xlna - 1(a > 1),
……6分 令F′ (x)= a xlna - 1≥0, 试题详情
解得:x ≥ 。 。 试题详情
所以当x ≥ 时:F′ (x)≥0,F (x)在区间 时:F′ (x)≥0,F (x)在区间 上是增函数; 上是增函数; 试题详情
当x ≤ 时:F′ (x)≤0,F (x)在区间 时:F′ (x)≤0,F (x)在区间 上是减函数。 上是减函数。 试题详情
试题详情
试题详情
故当a> 时:F (x)min =F ( 时:F (x)min =F ( )>0,所以方程F (x)=a x-x
=0无实数解,这说明函数f (x)=a x (a>1)的图像与直线y=x没有公共点; …10分 )>0,所以方程F (x)=a x-x
=0无实数解,这说明函数f (x)=a x (a>1)的图像与直线y=x没有公共点; …10分 试题详情
试题详情
试题详情
F (x)=a x-x(a>1)的单调性可知:-∞<0< < < < < <+∞,这说明函数f (x)=a x (a>1)的图像与直线y=x有两不同的公共点个公共点。 …12分 <+∞,这说明函数f (x)=a x (a>1)的图像与直线y=x有两不同的公共点个公共点。 …12分
综上所述: 试题详情
当a> 时: 函数f (x)=a x (a>1)与其反函数f -1 (x)=logax图像没有公共点; 时: 函数f (x)=a x (a>1)与其反函数f -1 (x)=logax图像没有公共点; 试题详情
当a = 时:函数f (x)=a x (a>1)与其反函数f -1 (x)=logax图像有唯一公共点; 时:函数f (x)=a x (a>1)与其反函数f -1 (x)=logax图像有唯一公共点; 试题详情
当1<a< 时:函数f (x)=a x (a>1)与其反函数f -1 (x)=logax图像有两个不同的公共点。
--13分 时:函数f (x)=a x (a>1)与其反函数f -1 (x)=logax图像有两个不同的公共点。
--13分 试题详情
试题详情
 ∪ ∪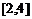
(1)求a,b,c。 试题详情
(2)是否存在实数m使不等式 对一切 对一切 成立?若存在,求出m的取值范围;若不存在,请说明理由。 成立?若存在,求出m的取值范围;若不存在,请说明理由。 试题详情
解:(1)∵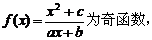 试题详情
∴ ……1分 ……1分 试题详情
∵ 的解集中包含2和-2,
的解集中包含2和-2, 试题详情
试题详情
即得 所以 所以 ……2分 ……2分 试题详情
∵ ∴ ∴ ……3分 ……3分 试题详情
下证:当a>0时,在(0,+∞)上 是增函数。 是增函数。 在(0,+∞)内任取x1,x2,且x1<x2,那么 试题详情
试题详情
即 …5分 …5分 试题详情
 所以, 所以,
试题详情
综上所述: ……6分
……6分 试题详情
(2)∵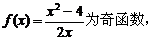 试题详情
∴ 在(-∞,0)上也是增函数。 …7分 在(-∞,0)上也是增函数。 …7分 试题详情
试题详情
所以,m为任意实数时,不等式 ……12分 ……12分 试题详情
19. 某旅游商品生产企业,2007年某商品生产的投入成本为1元/件,出厂价为流程图的输 试题详情
试题详情
(Ⅰ)写出2008年预计的年利润 与投入成本增加的比例 与投入成本增加的比例 的关系式; 的关系式; 试题详情
(Ⅱ)为使2008年的年利润比2007年有所增加,问:投入成本增加的比例 应在什么范围内? 应在什么范围内? 试题详情
试题详情
解:(Ⅰ)由流程图可知: .依题意,得 .依题意,得 试题详情
试题详情
 ( ( ); ); (Ⅱ)要保证2008年的利润比2007年有所增加,当且仅当 试题详情
 ,即 ,即 . .
试题详情
解之得 . . 试题详情
试题详情
(1) 若函数 为理想函数,求 为理想函数,求 的值; 的值; 试题详情
(2)判断函数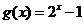  是否为理想函数,并予以证明; 是否为理想函数,并予以证明; 试题详情
试题详情
解:(1)取 可得 可得 .---------------1分 .---------------1分 试题详情
又由条件① ,故 ,故 .---------------3分 .---------------3分 试题详情
(2)显然 在[0,1]满足条件① 在[0,1]满足条件① ;---------------4分 ;---------------4分 试题详情
也满足条件② .---------5分 .---------5分 试题详情
试题详情
试题详情
 ,即满足条件③,---------------8分 ,即满足条件③,---------------8分
试题详情
故 理想函数. ---------------9分 理想函数. ---------------9分 试题详情
试题详情
 . --------------11分 . --------------11分
试题详情
若 ,则 ,则 ,前后矛盾;--------------12分 ,前后矛盾;--------------12分 试题详情
若 ,则 ,则 ,前后矛盾.--------------13分 ,前后矛盾.--------------13分 试题详情
故 . --------------14分 . --------------14分 (用其他方法解答的,请参照给分.) 试题详情
21. 已知函数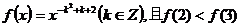 试题详情
Ⅰ)求 的值; 的值; 试题详情
试题详情
解:Ⅰ)由题意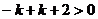 试题详情
试题详情
试题详情
试题详情
试题详情
Ⅱ)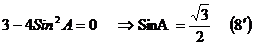 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
22. 设函数 求证: 求证: 试题详情
(1) ; ; 试题详情
(2)函数 在区间(0,2)内至少有一个零点; 在区间(0,2)内至少有一个零点; 试题详情
试题详情
证明:(1) 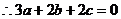 试题详情
又   ……………………2分 ……………………2分 又2c=-3a-2b 由3a>2c>2b ∴3a>-3a-2b>2b 试题详情
∵a>0  ………………………………………………4分 ………………………………………………4分 (2)∵f(0)=c,f(2)=4a+2b+c=a-c………………………………6分 试题详情
①当c>0时,∵a>0,∴f(0)=c>0且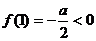 ∴函数f(x)在区间(0,1)内至少有一个零点……………………8分 试题详情
②当c≤0时,∵a>0 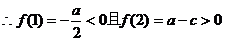 ∴函数f(x)在区间(1,2)内至少有一个零点. 综合①②得f(x)在(0,2)内至少有一个零点…………………………10分 (3)∵x1,x2是函数f(x)的两个零点 试题详情
则 的两根 的两根 试题详情
∴ ……………………………………12分 ……………………………………12分 试题详情
试题详情
试题详情
 ……………………………………16分 ……………………………………16分
试题详情
23. 为研究“原函数图象与其反函数图象的交点是否在直线 上”这个课题,我们可以分三步进行研究: 上”这个课题,我们可以分三步进行研究: (I)首先选取如下函数: 试题详情
试题详情
 与其反函数 与其反函数 的交点坐标为(-1,-1) 的交点坐标为(-1,-1) 试题详情
 与其反函数 与其反函数 的交点坐标为(0,0),(1,1) 的交点坐标为(0,0),(1,1) 试题详情
 与其反函数 与其反函数 的交点坐标为( 的交点坐标为( ),(-1,0),(0,-1) ),(-1,0),(0,-1) (II)观察分析上述结果得到研究结论; (III)对得到的结论进行证明。 现在,请你完成(II)和(III)。 解:(II)原函数图象与其反函数图象的交点不一定在直线y=x上 2分 试题详情
(III)证明:设点(a,b)是 的图象与其反函数图象的任一交点,由于原函数与反函数图象关于直线y=x对称,则点(b,a)也是 的图象与其反函数图象的任一交点,由于原函数与反函数图象关于直线y=x对称,则点(b,a)也是 的图象与其反函数图象的交点,且有 的图象与其反函数图象的交点,且有 试题详情
试题详情
若a=b时,交点显然在直线 上 上 试题详情
试题详情
试题详情
试题详情
如果函数 是减函数,并且 是减函数,并且 的图象与其反函数的图象有交点,则交点不一定在直线y=x上。 14分 的图象与其反函数的图象有交点,则交点不一定在直线y=x上。 14分 试题详情
24. 用水清洗一堆蔬菜上残留的农药的效果假定如下:用x单位量的水清洗一次以后,蔬菜上残留的农药量与这次清洗前残留的农药量之比为 . . 试题详情
(Ⅰ)试解释 的实际意义; 的实际意义; (Ⅱ)现有a(a>0)单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次.哪种方案清洗后蔬菜上残留的农药比较少?请说明理由. 试题详情
答案:解:(I)f(0)=1.表示没有用水清洗时,蔬菜上的农药量没有变化.……………2' 试题详情
(Ⅱ)设清洗前蔬菜上的农药量为1,那么用a单位量的水清洗1次后.残留的农药量为 W1=1×f(a)= ;……………………………………………………………………4' ;……………………………………………………………………4' 试题详情
试题详情
此后再用 单位量的水清洗1次后,残留的农药量为 单位量的水清洗1次后,残留的农药量为 试题详情
试题详情
试题详情
试题详情
试题详情
(1)若t=1且 ,求实数x的值; ,求实数x的值; 试题详情
(2)对tÎR写出函数 具备的性质. 具备的性质. 试题详情
解:(1)由已知得 ……2分
……2分 试题详情
 ……4分
……4分
试题详情
解得 ,或 ,或 ……6分
……6分 试题详情
(2) ……8分
……8分 具备的性质: ①偶函数; 试题详情
试题详情
试题详情
说明:写出一个性质得3分,写出两个性质得5分,写出三个性质得6分,包括写出函数的零点( , , )等皆可。写出函数的定义域不得分,写错扣1分 )等皆可。写出函数的定义域不得分,写错扣1分 试题详情
26. 已知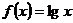 试题详情
(1) , 求 , 求 的最小值 的最小值 试题详情
(2)P、Q关于点(1,2)对称,若点P在曲线C上移动时,点Q的轨迹是函数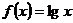 的图象,求曲线C的轨迹方程。 的图象,求曲线C的轨迹方程。 试题详情
(3)在中学数学中,从特殊到一般,从具体到抽象是常见的一种思维形式。如从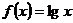 可抽象出 可抽象出 的性质,试分别写出一个具体的函数,抽象出下列相应的性质 的性质,试分别写出一个具体的函数,抽象出下列相应的性质 试题详情
由 可抽象出 可抽象出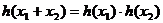 试题详情
由 可抽象出 可抽象出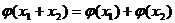 试题详情
(1)  …………3’ …………3’ 试题详情
等号当x=2时成立,  …………………………4’ …………………………4’ (2)设P(x,y)则Q(2-x,4-y)………………………………………………5’ 由4-y=lg(2-x)可得:y=4-lg(2-x)………………………………8’ (3) h(x)=_______y=2x等_______, φ(x)=____y=lgx等__ 试题详情
试题详情
点 在函数 在函数 的图像上移动. 的图像上移动. 试题详情
试题详情
(2) 求函数 的解析式; 的解析式; 试题详情
试题详情
 时有最小值而没有最大值. 时有最小值而没有最大值.
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
28. 对于在区间[m,n]上有意义的两个函数f (x)与g (x),如果对任意x∈[m,n]均有| f
(x) ? g (x) |≤1,则称f (x)与g (x)在[m,n]上是接近的,否则称f (x)与g (x)在[m,n]上是非接近的,现有两个函数f 1(x)
= loga(x ? 3a)与f 2 (x)
= loga (a > 0,a≠1),给定区间[a
+ 2,a + 3]. (a > 0,a≠1),给定区间[a
+ 2,a + 3]. (1)若f 1(x)与f 2 (x)在给定区间[a
+ 2,a + 3]上都有意义,求a的取值范围; (2)讨论f 1(x)与f 2 (x)在给定区间[a
+ 2,a + 3]上是否是接近的? 解:(1)要使f 1 (x)与f 2 (x)有意义,则有 试题详情
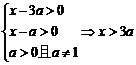 要使f 1 (x)与f 2 (x)在给定区间[a
+ 2,a + 3]上有意义, 等价于真数的最小值大于0 试题详情
即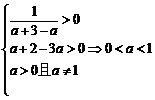 (2)f 1 (x)与f 2 (x)在给定区间[a
+ 2,a + 3]上是接近的 试题详情
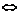 | f 1 (x) ? f 2 (x)|≤1 | f 1 (x) ? f 2 (x)|≤1
试题详情
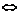  ≤1 ≤1
试题详情
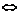 |loga[(x ? 3a)(x ? a)]|≤1 |loga[(x ? 3a)(x ? a)]|≤1
试题详情
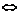 a≤(x ? 2a)2
? a2≤ a≤(x ? 2a)2
? a2≤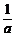
对于任意x∈[a + 2,a + 3]恒成立 设h(x)
= (x ? 2a)2 ? a2,x∈[a
+ 2,a + 3] 试题详情
 且其对称轴x = 2a
< 2在区间[a + 2,a + 3]的左边 且其对称轴x = 2a
< 2在区间[a + 2,a + 3]的左边
试题详情
试题详情
试题详情
试题详情
试题详情
当 时 时 f 1 (x)与f 2
(x)在给定区间[a + 2,a + 3]上是接近的 试题详情
当 < a < 1时,f 1 (x)与f 2
(x)在给定区间[a + 2,a + 3]上是非接近的. < a < 1时,f 1 (x)与f 2
(x)在给定区间[a + 2,a + 3]上是非接近的. 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
(2)当 ∈(-∞,-3)时, ∈(-∞,-3)时, 是减函数, 是减函数, 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
30. 我国是水资源匮乏的国家,为鼓励节约用水,某市打算出台一项水费政策措施,规定:每季度每人用水量不超过5吨时,每吨水费收基本价1.3元;若超过5吨而不超过6吨时,超过部分水费加收200%;若超过6吨而不超过7吨时,超过部分的水费加收400%。如果某人本季度实际用水量为 吨,应交水费为 吨,应交水费为 。 。 试题详情
(Ⅰ)求 的值; 的值; 试题详情
(Ⅱ)试求出函数 的解析式。 的解析式。 试题详情
解:(1) -----------------------------2分 -----------------------------2分 试题详情
 ----------------------------4分 ----------------------------4分
试题详情
 ---------------6分 ---------------6分
试题详情
(2)当 时, 时, --------------7分 --------------7分 试题详情
当 时, 时, ----------------------9分 ----------------------9分 试题详情
当 时, 时, --------11分 --------11分 试题详情
故 ----------------------------12分 ----------------------------12分 试题详情
31. 已知函数 为奇函数, 为奇函数, 试题详情
1)
求实数 的值; 的值; 试题详情
2)
求 的反函数 的反函数 ; ; 试题详情
试题详情
试题详情
 上是否分离?若分离,求出 上是否分离?若分离,求出 的取值范围;若不分离,请说明理由; 的取值范围;若不分离,请说明理由;
试题详情
1) 为奇函数 为奇函数 试题详情
2) 试题详情
3) 试题详情
试题详情
试题详情
 ; ;
试题详情
试题详情
 ; ;
试题详情
故 的取值范围是: 的取值范围是: ; ; 试题详情
试题详情
试题详情
(Ⅲ)求函数 的值域. 的值域. 试题详情
解:(1)由 ,得 ,得 ,……………………………………………….1分 ,……………………………………………….1分 试题详情
由 ,得 ,得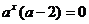 试题详情
由 得 得 ,………………………………………………………………….2分 ,………………………………………………………………….2分 试题详情
 …………………………………………………………………….1分 …………………………………………………………………….1分
试题详情
(2) ( ( )……………………………………….4分 )……………………………………….4分 试题详情
(3)由已知得, .………………………….1分 .………………………….1分 试题详情
试题详情
试题详情
33. 某厂预计从2008年初开始的前n个月内,市场对某种产品的需求总量f(n)与月份n的近似关系为:f(n)=n(n+1)(35-2n), (单位:台),n∈N*,且n≤12 ⑴写出2008年第n个月的需求量g(n)与月份n的关系式 ⑵如果该厂此种产品每月生产a台,为保证每月满足市场需求,则a至少应为多少? ⑴g(n)=-6x2+72x,⑵216;. 试题详情
34、设函数 = = ,其中 ,其中 试题详情
 . . 试题详情
(1)在实数集 上用分段函数形式写出函数 上用分段函数形式写出函数 的解析式; 的解析式; 试题详情
(2)求函数 的最小值. 的最小值. 试题详情
解:(1) = = ,(1分) ,(1分) 试题详情
令 ,得 ,得 ,(3分) ,(3分) 试题详情
试题详情
(写出 4分) 4分) 试题详情
试题详情
同理,当 ;(12分) ;(12分) 试题详情
又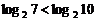  .(14分) .(14分) 试题详情
或解:因为 是偶函数,所以只需要考虑 是偶函数,所以只需要考虑 的情形,(9分) 的情形,(9分) 试题详情
当 ;(11分) ;(11分) 试题详情
试题详情
 .(14分) .(14分)
试题详情
试题详情
| 
 的解为
. 5
的解为
. 5 ,则使函数
,则使函数 的定义域为R且在(-∞,0)上单调递增的
的定义域为R且在(-∞,0)上单调递增的 值为 .
值为 .
 对任意的正实数x成立,则
对任意的正实数x成立,则

 .2009
.2009 ,函数
,函数 的定义域为Q.
的定义域为Q. ,则实数a的值为
,则实数a的值为  ;
; ,则实数a的取值范围为
,则实数a的取值范围为  .
. 的正负_______________正数
的正负_______________正数 是奇函数且周期为3,
是奇函数且周期为3, = .1
= .1 (
( ),则
),则 .
.
 的值域是 .
的值域是 .
 (
( 且
且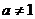 )与函数
)与函数 (
( 且
且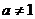 )的定义域相同;
)的定义域相同; (
( 为常数)的图像可由函数
为常数)的图像可由函数 的图像经过平移得到;
的图像经过平移得到; (
( )是奇函数且函数
)是奇函数且函数 (
( )是偶函数;
)是偶函数; 是周期函数.其中正确结论的序号是___________________.(填写你认为正确的所有结论序号)①②③④
是周期函数.其中正确结论的序号是___________________.(填写你认为正确的所有结论序号)①②③④ ,则f(x)的奇偶性一定是
. 偶函数
,则f(x)的奇偶性一定是
. 偶函数 的图像与函数
的图像与函数 的图像交点的坐标是 ;
的图像交点的坐标是 ;
 是定义域为
是定义域为 的奇函数,在区
的奇函数,在区 间
间 上单调递增,当
上单调递增,当 时,
时, 的图像如右图所示:
的图像如右图所示: ,则
,则 的取值范围是
;
的取值范围是
; ;
; :
: 。现有点
。现有点 与
与 ,点
,点 是线段
是线段 上一动点,按定义的对应法则
上一动点,按定义的对应法则 :
: 。当点
。当点 在线段
在线段 上从点
上从点 开始运动到点
开始运动到点 结束时,点
结束时,点 的对应点
的对应点 所经过的路线长度为
。
所经过的路线长度为
。 。
。 满足
满足 ,且
,且 时,
时, ,则函数
,则函数 的图象与函数
的图象与函数 的图象的交点的个数是 .
4
的图象的交点的个数是 .
4 的定义域为
的定义域为 ,若存在常数
,若存在常数 ,使
,使
 对一切实数
对一切实数 均成立,则称
均成立,则称 为“海宝”函数。给出下列函数:
为“海宝”函数。给出下列函数: ②
② ③
③
 ④
④
 是“海宝”函数的序号为
. ③
是“海宝”函数的序号为
. ③ (
( >0
,
>0
,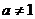 )是R上的增函数,那么
)是R上的增函数,那么 的取值范围是
.
的取值范围是
.
 为偶函数,则实数
为偶函数,则实数 的值是
.1
的值是
.1 (
( >1)的值域是
.
>1)的值域是
.

 满足
满足 ,且
,且
 6
6
 (x>1,p为正常数),
(x>1,p为正常数), 有相同值域,则P的值为
。
有相同值域,则P的值为
。
 是定义域为R的偶函数,其图象关于直线x=2对称,当
是定义域为R的偶函数,其图象关于直线x=2对称,当 时,
时, ,则
,则 的表达式为
的表达式为 
 的值=
8204
的值=
8204 与
与 :
: 关于直线
关于直线 对称,且图象
对称,且图象 关于
关于 对称,则
对称,则 的值为
.2
的值为
.2 根据上述促销方法,顾客在该商场购物可以获得双重优惠,例如,购买标价为400元的商品,则消费金额为320元,获得的优惠额为:400×0.2+30=110(元).若顾客购买一件标价为1000元的商品,则所能得到的优惠额为( )
根据上述促销方法,顾客在该商场购物可以获得双重优惠,例如,购买标价为400元的商品,则消费金额为320元,获得的优惠额为:400×0.2+30=110(元).若顾客购买一件标价为1000元的商品,则所能得到的优惠额为( ) 的图象如右图所示,
的图象如右图所示, = _ 27
= _ 27 ,若关于
,若关于 的方程
的方程 恰有5个不同的实数解x1、x2、x3、x4、x5则f(x1+x2+x3+x4+x5)等于 _ 3lg2
恰有5个不同的实数解x1、x2、x3、x4、x5则f(x1+x2+x3+x4+x5)等于 _ 3lg2 是定义在
是定义在 上的函数,给定下列三个条件:(1)
上的函数,给定下列三个条件:(1) 是偶函数;(2)
是偶函数;(2) 的图象关于直线
的图象关于直线 对称;(3)
对称;(3) 为
为 的一个周期.如果将上
的一个周期.如果将上 的根
的根 ,
, ∈Z,则
∈Z,则 =
3
=
3

 在
在 的近似解的程序框图,要求解的精确度为
的近似解的程序框图,要求解的精确度为 ,①处填的内容是____________, ②处填的内容是______________________.
,①处填的内容是____________, ②处填的内容是______________________. ,
,
 的定义域为
的定义域为 ,则
,则 =
0
=
0 为偶函数,则实数
为偶函数,则实数 的值是
.1
的值是
.1 的反函数图像恒过定点A,过点A的直线
的反函数图像恒过定点A,过点A的直线 与圆
与圆 相切,则直线
相切,则直线 的方程是
.y=1
的方程是
.y=1 已知定义在区间
已知定义在区间 上的函数
上的函数 的图像如图所示,对于满足
的图像如图所示,对于满足 的任意
的任意 、
、 ,给出下列结论:
,给出下列结论: ;
; ;
; .
. , 都有
, 都有 答:
.
答:
. 等等.
等等. ,
, 成立,则实数a的取值范围是
。
成立,则实数a的取值范围是
。
 34. 幂函数y=xa,当a取不同的正数时,在区间[0,1]上它们的图像是一族美丽的曲线(如图).设点A(1,0),B(0,1),连接AB,线段AB恰好被其中的两个幂函数y=xa,y=xb的图像三等分,即有BM=MN=NA.那么,ab=
.1.
34. 幂函数y=xa,当a取不同的正数时,在区间[0,1]上它们的图像是一族美丽的曲线(如图).设点A(1,0),B(0,1),连接AB,线段AB恰好被其中的两个幂函数y=xa,y=xb的图像三等分,即有BM=MN=NA.那么,ab=
.1. .
. (x∈[-8π,8π])的最大值为M,最小值为m,则M+m=
.2
(x∈[-8π,8π])的最大值为M,最小值为m,则M+m=
.2 是
是 上奇函数,
上奇函数,  上分别递减和递增,则不等式
上分别递减和递增,则不等式 的解集为
的解集为
 ,【
,【 】表示不超过实数
】表示不超过实数 的最大整数,则函数【
的最大整数,则函数【 】
】 【
【 】的值域是_________.
】的值域是_________. ∴
∴
 】
】 【
【 】=【
】=【 】
】 【
【 】,即【
】,即【 】
】 【
【 】
】 为整数时,值为
为整数时,值为 ;当
;当 为小数时,值为
为小数时,值为 ;故所求值域为
;故所求值域为
 上是增函数,在区间[3,6]上的最大值为8,最小值为-1,则
上是增函数,在区间[3,6]上的最大值为8,最小值为-1,则 =
=  .
. 的长度
的长度 。已知函数
。已知函数 的定义域为
的定义域为 ,值域为
,值域为 ,则区间
,则区间 的长度的最大值与最小值的差为_________.3
的长度的最大值与最小值的差为_________.3 ,[x]表示不大于x的最大整数,如
,[x]表示不大于x的最大整数,如 ,
, ,
, ,则
,则 _____________;使
_____________;使 成立的x的取值范围是_____________ 答案:2
成立的x的取值范围是_____________ 答案:2 ,若|m-1|※m=|m-1|,则m的取值范围是
,若|m-1|※m=|m-1|,则m的取值范围是
 ,定义运算
,定义运算 ,其中
,其中 为常数,等号右边的运算是通常意义的加、乘运算。现已知
为常数,等号右边的运算是通常意义的加、乘运算。现已知 ,且有一个非零实数
,且有一个非零实数 ,使得对任意实数
,使得对任意实数 ,都有
,都有 ,则
,则
 。
。 ,符号[
,符号[ ]表示
]表示 的整数部分,即[
的整数部分,即[ ]是不超过
]是不超过 的最大整数”。在实数轴R(箭头向右)上[
的最大整数”。在实数轴R(箭头向右)上[ ]是在点
]是在点 左侧的第一个整数点,当
左侧的第一个整数点,当 是整数时[
是整数时[ ]就是
]就是 。这个函数[
。这个函数[ ]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用。那么
]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用。那么 =___________________
=___________________ ,记
,记 ,(其中
,(其中 ),例如:
),例如:
 。设
。设 ,且满足
,且满足 ,则有序数组
,则有序数组
 。
。 
 是定义在
是定义在 -∞,+∞
-∞,+∞ 上的函数,
上的函数, ∈
∈ -∞,+∞
-∞,+∞ ,请给出能使命题:“若
,请给出能使命题:“若 +1>0,则
+1>0,则 +
+ >
> +
+ ”成立的一个充分条件:
”成立的一个充分条件: 是定义在
是定义在 -∞,+∞
-∞,+∞ 上的函数,
上的函数, ∈
∈ -∞,+∞
-∞,+∞ ,请给出能使命题:“若
,请给出能使命题:“若 +1>0,则
+1>0,则 +
+ >
> +
+ ”成立的一个充分条件:_______.
”成立的一个充分条件:_______. 在
在 -∞,+∞
-∞,+∞ 上单调递增(或
上单调递增(或 =
= +
+ (
( >0)等)
>0)等) 年前死亡的,则
年前死亡的,则 满足的等式为
,
满足的等式为
, 用自然对数的运算式子可以表示为
.(只写出运算式子不需要计算出结果,式子中可以出现自然对数、实数之间的四则运算.提示:
用自然对数的运算式子可以表示为
.(只写出运算式子不需要计算出结果,式子中可以出现自然对数、实数之间的四则运算.提示:  )
) 、(
、( )
)

 的单调增区间是
。
的单调增区间是
。 
 的最大值与最小值分别为M,m,则M+m= 6
的最大值与最小值分别为M,m,则M+m= 6  在区间
在区间 上是增函数的充要条件是_______________.
上是增函数的充要条件是_______________.
 的一组解为
的一组解为

 -
- 的解是 .
的解是 .
 的值域是R,则实数
的值域是R,则实数 的取值范围是
.
的取值范围是
.
 的两根为
的两根为 、
、 ,且
,且 ,则
,则 的最小值是
4
的最小值是
4
 的图像大致是……………………………………( B )
的图像大致是……………………………………( B )
